五年级数学思维导图如何帮孩子理清知识脉络？

小学五年级数学（上册）思维导图

中心主题：小学五年级数学（上册）知识体系

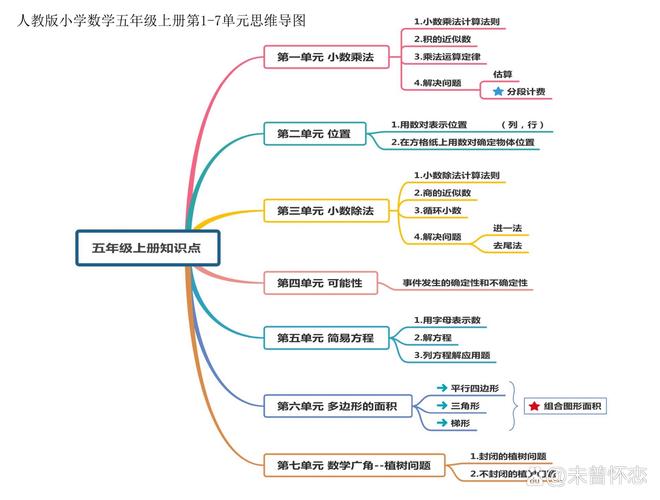
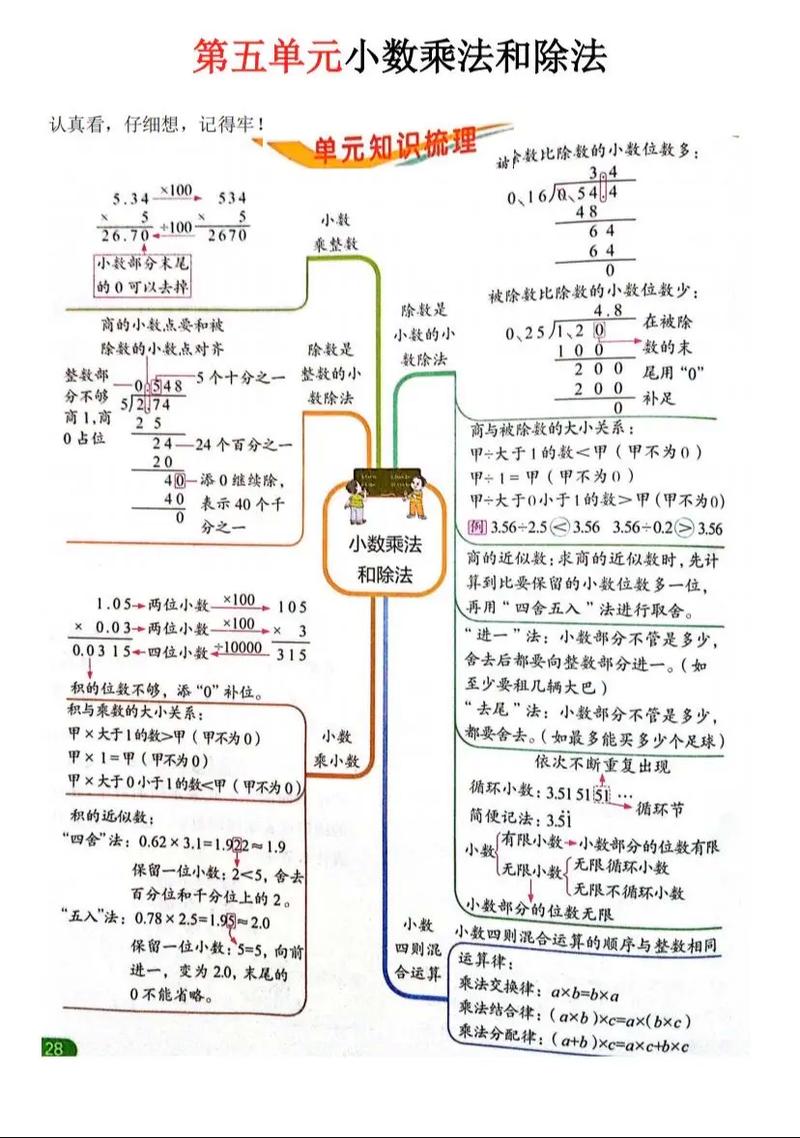
第一单元：小数乘法

• 核心概念
  • 意义：求几个相同加数和的简便运算,或求一个数的几倍是多少。
  • 法则
    • 整数乘法：按整数乘法法则算出积。
    • 小数点处理：看因数中一共有几位小数，就从积的右边起数出几位,点上小数点。
    • 特殊情况：积的小数位数不够时，要用“0”补足；末尾有“0”的要化简。
  • 应用
    • 求近似数：根据需要，用“四舍五入”法求积的近似数。
    • 连乘、乘加、乘减：运算顺序与整数相同,有括号的先算括号里的。
    • 整数乘法运算定律推广到小数
      • 交换律：a × b = b × a
      • 结合律：(a × b) × c = a × (b × c)
      • 分配律：(a + b) × c = a × c + b × c

第二单元：位置

• 核心概念
  • 用数对确定位置
    • 表示方法：(列数, 行数)
    • 关键点：先列后行，用逗号隔开,外面加括号。
    • 应用：在方格图中,可以用数对精确表示一个点的位置。
  • 图形平移与坐标变化
    • 列不变：上下平移,行数发生变化。
    • 行不变：左右平移,列数发生变化。
    • 规律：图形向哪个方向平移,哪个方向的坐标就相应增加或减少。

第三单元：小数除法

• 核心概念
  • 意义：已知两个因数的积与其中一个因数,求另一个因数的运算。
  • 法则
    • 除数是整数：按整数除法法则去除，商的小数点要和被除数的小数点对齐，如果除到被除数的末尾仍有余数，就在余数后面添“0”继续除。
    • 除数是小数：先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也向右移动几位（位数不够的，用“0”补足）；然后按“除数是整数”的方法计算。
  • 应用
    • 求近似数：用“四舍五入”法求商的近似数,根据要求保留一定的小数位数。
    • 循环小数：一个数的小数部分，从某一位起，一个数字或几个数字依次不断重复出现。
      • 循环节：重复出现的数字。
      • 表示方法：在循节的首位和末位数字上各点一个圆点。
    • 用计算器探索规律：用计算器计算,发现数字排列的规律。
    • 解决问题：结合实际情况，灵活运用小数除法解决生活中的问题（如单价、速度等）。

第四单元：简易方程

• 核心概念
  • 用字母表示数
    • 表示数量关系：如 s = v × t (路程 = 速度 × 时间)。
    • 表示计算公式：如 c = (a + b) × 2 (长方形周长 = (长 + 宽) × 2)。
    • 注意事项：数字和字母相乘，省略乘号，数字在前；字母和字母相乘，省略乘号；1与任何字母相乘,1省略。
  • 方程的意义
    • 方程：含有未知数的等式。
    • 方程的解：使方程左右两边相等的未知数的值。
    • 解方程：求方程的解的过程。
  • 解方程
    • 原理：等式的性质（方程两边同时加上、减去、乘以或除以同一个不为0的数，方程左右两边仍然相等）。
    • 方法：通过变形，将方程最终化为 x = a 的形式。
  • 列方程解决问题
    • 步骤：
      1. 审题：理解题意,找出等量关系。
      2. 设未知数：用字母表示未知数。
      3. 列方程：根据等量关系列出方程。
      4. 解方程：求出未知数的值。
      5. 检验并作答：检查答案是否符合题意,写出答案。

第五单元：多边形的面积

• 核心概念
  • 平行四边形的面积
    • 公式：S = a × h (底 × 高)
    • 推导：通过“割补法”将平行四边形转化为长方形。
  • 三角形的面积
    • 公式：S = a × h ÷ 2 (底 × 高 ÷ 2)
    • 推导：两个完全相同的三角形可以拼成一个平行四边形。
  • 梯形的面积
    • 公式：S = (a + b) × h ÷ 2 ((上底 + 下底) × 高 ÷ 2)
    • 推导：两个完全相同的梯形可以拼成一个平行四边形。
  • 组合图形的面积
    • 方法：分割法、添补法。
    • 关键：将组合图形转化为已学过的简单图形（长方形、正方形、平行四边形、三角形、梯形）,然后计算各部分面积之和或差。

第六单元：统计与可能性

• 核心概念
  • 中位数
    • 定义：将一组数据按大小顺序排列，处于最中间位置的一个数（或最中间两个数的平均数）。
    • 特点：不受偏大或偏小数据的影响，能反映数据的“一般水平”。
  • 可能性
    • 事件分类：必然事件、不可能事件、不确定事件。
    • 可能性大小：事件发生的可能性有大有小,可以用分数来表示。
    • 等可能性：在所有结果中,每个结果出现的可能性都相等。
    • 游戏规则的公平性：使事件发生的可能性相等,游戏规则才公平。

第七单元：数学广角——植树问题

• 核心概念
  • 关键：明确“间隔数”与“棵数”之间的关系。
  • 三种情况
    • 两端都栽：棵数 = 间隔数 + 1
    • 一端栽，一端不栽：棵数 = 间隔数
    • 两端都不栽：棵数 = 间隔数 - 1
  • 应用：解决生活中类似的问题，如安装路灯、锯木头、爬楼梯、钟表敲响等。

第八单元：总复习

• 知识梳理与巩固
  • 小数乘除法：法则、混合运算、简便运算。
  • 简易方程：用字母表示数、解方程、列方程解决问题。
  • 多边形的面积：各图形面积公式的推导、应用及组合图形面积计算。
  • 位置与可能性：数对、中位数、事件可能性。

小学五年级数学（下册）思维导图

中心主题：小学五年级数学（下册）知识体系

第一单元：观察物体（三）

• 核心概念
  • 从不同方向观察立体图形
    • 特征：从一个方向看到的形状,不能确定唯一的立体图形。
    • 策略：根据从一个方向看到的形状，结合其他方向的信息,进行推理和搭建。
  • 根据平面图形还原立体图形
    • 方法：先确定底层，再根据上层的信息进行搭建,需要空间想象能力。

第二单元：因数与倍数

• 核心概念
  • 因数和倍数
    • 关系：a × b = c (a, b, c为非0自然数)，那么a和b是c的因数,c是a和b的倍数。
    • 特点：一个数的因数是有限的，其中最小的是1，最大的是它本身，一个数的倍数是无限的,其中最小的是它本身。
  • 2, 5, 3的倍数的特征
    • 2的倍数（偶数）：个位上是0, 2, 4, 6, 8。
    • 5的倍数：个位上是0或5。
    • 3的倍数：各位上的数字之和是3的倍数。
  • 质数和合数
    • 质数（素数）：只有1和它本身两个因数。
    • 合数：除了1和它本身,还有其他因数。
    • 1的特殊性：1既不是质数也不是合数。
  • 分解质因数
    • 定义：把一个合数用质因数相乘的形式表示出来。
    • 方法：短除法。

第三单元：长方体和正方体

• 核心概念
  • 认识长方体和正方体
    • 特征：面、棱、顶点。
    • 关系：正方体是特殊的长方体（长、宽、高都相等）。
  • 表面积
    • 长方体表面积：S = (ab + ah + bh) × 2 (长×宽 + 长×高 + 宽×高) × 2
    • 正方体表面积：S = 6a² (棱长 × 棱长 × 6)
  • 体积
    • 定义：物体所占空间的大小。
    • 单位：立方米 (m³)、立方分米 (dm³)、立方厘米 (cm³)，以及升 (L) 和毫升 (mL)。
    • 进率：1 m³ = 1000 dm³；1 dm³ = 1000 cm³；1 L = 1000 mL；1 dm³ = 1 L；1 cm³ = 1 mL。
    • 长方体体积：V = a × b × h (长 × 宽 × 高)
    • 正方体体积：V = a³ (棱长 × 棱长 × 棱长)
    • 容积：容器所能容纳物体的体积。
  • 不规则物体的体积测量
    • 方法：排水法（物体体积 = 上升水的体积）。

第四单元：分数的意义和性质

• 核心概念
  • 分数的意义
    • 单位“1”：一个物体、一些物体等都可以看作一个整体，这个整体叫做单位“1”。
    • 分数的意义：把单位“1”平均分成若干份,表示这样的一份或几份的数。
    • 分数单位：把单位“1”平均分成若干份,表示其中一份的数。
  • 分数与除法
    • 关系：被除数 ÷ 除数 = 被除数 / 除数 (除数 ≠ 0)
    • 应用：求一个数是另一个数的几分之几。
  • 真分数和假分数
    • 真分数：分子小于分母,小于1。
    • 假分数：分子大于或等于分母,大于或等于1。
    • 带分数：由整数部分和真分数部分组成。
  • 分数的基本性质
    • 性质：分数的分子和分母同时乘或除以相同的数（0除外）,分数的大小不变。
    • 应用：约分和通分。
  • 约分和通分
    • 最大公因数：几个数公有的因数中最大的一个。
    • 约分：把一个分数化成和它相等，但分子和分母都比较小的分数（最简分数）。
    • 最小公倍数：几个数公有的倍数中最小的一个。
    • 通分：把异分母分数分别化成和原来分数相等的同分母分数。
  • 分数和小数的互化
    • 小数化分数：先写成分母是10, 100, 1000...的分数,再化简。
    • 分数化小数：用分子除以分母，能化成有限小数的,分母只含有质因数2和5。

第五单元：图形的运动（三）

• 核心概念
  • 旋转
    • 三要素：旋转中心、旋转方向、旋转角度。
    • 特征：图形旋转后，形状、大小不变,位置和方向改变。
    • 性质：对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角相等。
  • 运用对称和旋转设计图案
    • 方法：利用轴对称、平移、旋转等运动方式组合设计。

第六单元：分数的加法和减法

• 核心概念
  • 同分母分数加、减法
    • 法则：分母不变，分子相加、减。
  • 异分母分数加、减法
    • 法则：先通分，化成同分母分数，再按照同分母分数加、减法计算。
  • 分数加减混合运算
    • 顺序：与整数加减混合运算顺序相同。
    • 简便运算：可以运用加法交换律、结合律进行简便计算。
  • 解决问题
    • 找单位“1”：关键在于理解题意，明确把谁看作单位“1”。
    • 类型：求一个数的几分之几是多少；求比一个数多（少）几分之几的数是多少等。

第七单元：折线统计图

• 核心概念
  • 单式折线统计图
    • 特点：用一个单位长度表示一定的数量，根据数量的多少描出各点,然后把各点用线段顺次连接起来。
    • 作用：不仅能表示出数量的多少,还能清楚地表示出数量的增减变化趋势。
  • 复式折线统计图
    • 特点：用不同的颜色（或线型）表示多组数据。
    • 作用：便于对两组数据进行比较和分析。

第八单元：数学广角——找次品

• 核心概念
  • 问题核心：从若干个外观相同的物品中找出一个质量不同的次品（轻或重）。
  • 最优策略
    • 原则：尽可能地将物品平均分成3份。
    • 原因：每次称重,都能最大范围地缩小次品所在的范围。
    • 规律：所需要称的最少次数，满足 3^n < 待测物品数 ≤ 3^(n+1),其中n为称的次数。

第九单元：总复习

• 知识梳理与巩固
  • 图形与几何：观察物体、长方体和正方体、图形的运动。
  • 数与代数：因数与倍数、分数的意义和性质、分数的加法和减法。
  • 统计与概率：折线统计图、找次品问题。

如何使用这份思维导图

1. 课前预习：看着导图的标题,尝试回忆每个单元的主要内容。
2. 课堂笔记：在对应的知识点下补充老师讲解的例题、易错点和解题技巧。
3. 课后复习：每周或每个单元结束后，看着导图进行“地毯式”复习,检查自己的知识盲点。
4. 考前冲刺：考前总览全图，快速回顾所有核心概念和公式,做到心中有数。

希望这份详细的思维导图能帮助五年级的同学更好地学习数学,建立清晰的数学知识网络！