概览

五年级上册的数学内容可以大致分为四个板块：小数乘法、简易方程、多边形的面积，以及数学广角和综合应用。

小学五年级数学课本上册
（图片来源网络，侵删）

第一单元：小数乘法

这是本学期的基础和重点,是整数乘法的延伸，也是后续学习小数除法的基础。

  • 核心知识点：

    1. 小数乘整数：

      • 意义： 求几个相同加数的和的简便运算（与整数乘法意义相同）。
      • 计算方法： 先按整数乘法算出积，再看因数中有几位小数，就从积的右边起数出几位，点上小数点。
      • 应用： 解决“求一个数的几倍是多少”或“求几个相同加数的和”等实际问题。

    2. 小数乘小数：

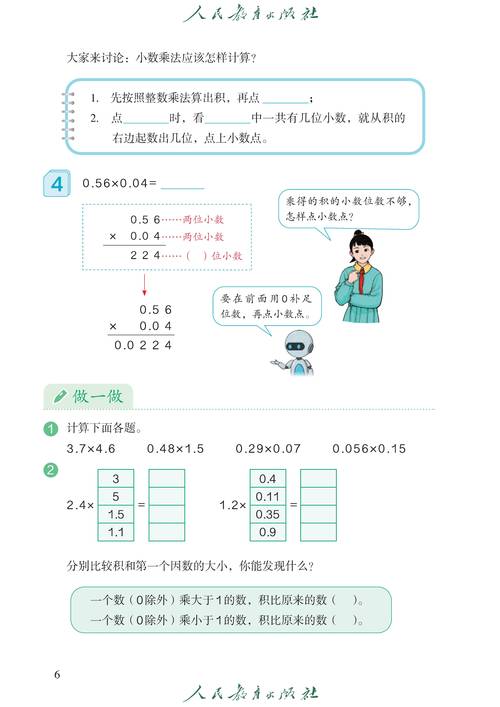      小学五年级数学课本上册
      （图片来源网络，侵删）
      • 意义： 可以理解为“求这个数的十分之几、百分之几……”。
      • 计算方法： 先按整数乘法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点，如果积的小数位数不够，要在前面用“0”补足，再点小数点。
      • 重点与难点： 积的小数点位置的确定，以及“0”的处理。

    3. 积的近似数：

      • 方法： 根据题目要求，用“四舍五入”法求积的近似数，要看需要保留的小数位数下一位的数字来决定是“舍”还是“入”。

    4. 整数乘法运算定律推广到小数：

      • 定律： 交换律 (a×b = b×a)、结合律 ((a×b)×c = a×(b×c))、分配律 ((a+b)×c = a×c + b×c)。
      • 应用： 运用这些定律可以使一些小数计算变得简便。

    5. 解决问题：

      • 类型： 主要涉及“归一问题”（先求单一量，再求总量）和“归总问题”（先求总量，再求单一量）。
      • 典型问题： “每千克苹果x元，买y千克要多少钱？”或者“买一定数量的商品花了多少钱，如果单价变化，能买多少？”

第二单元：位置

这是小学阶段第一次正式用“数对”来确定位置，为后续学习坐标系打下基础。

小学五年级数学课本上册
（图片来源网络，侵删）
  • 核心知识点：
    1. 用数对表示位置：
      • 方法： 用 (列数, 行数) 的形式来确定物体在平面上的位置。
      • 关键： 列数在前，行数在后，中间用逗号隔开，外面加上括号。
      • 举例： 教室里小明坐在第3列第4行，他的位置用数对表示就是 (3, 4)。

第三单元：小数除法

本单元的另一个重点,与“小数乘法”并列，是计算能力的核心训练。

  • 核心知识点：

    1. 除数是整数的小数除法：

      • 计算方法： 按照整数除法的法则去除，商的小数点要和被除数的小数点对齐，如果除到被除数的末尾仍有余数，就在余数后面添“0”继续除。
      • 特殊情况： 如果整数部分不够除，商要写“0”，点上小数点再继续除。

    2. 一个数除以小数：

      • 计算方法： 先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也向右移动几位（位数不够的，在被除数的末尾用“0”补足）；然后按照除数是整数的小数除法进行计算。
      • 重点与难点： 小数点移动的位数和方向，以及“0”的补足。

    3. 商的近似数：

      • 方法： 与“积的近似数”类似，用“四舍五入”法，但要注意，除法过程中，要比需要保留的小数位数多除一位。

    4. 循环小数：

      • 概念： 一个小数，从小数部分的某一位起，一个数字或者几个数字依次不断地重复出现，这样的小数叫做循环小数。
      • 表示方法： 用“循环节”上方加圆点来表示，0.333... 写作 3̇，0.585858... 写作 58̇。

    5. 用计算器探索规律：

      • 目的： 培养学生使用计算器进行探索和发现规律的能力。

    6. 解决问题：

      • 类型： “进一法”（如装东西，无论剩余多少，都需要一个额外的容器）和“去尾法”（如买东西，钱不够就不能买）的实际应用，这是对“四舍五入”的补充和拓展。

第四单元：可能性

这是一个关于概率和统计的初步认识单元,比较有趣。

  • 核心知识点：
    1. 事件发生的确定性与不确定性：
      • 确定事件： 一定会发生（必然事件）或一定不会发生（不可能事件）。
      • 不确定事件： 可能发生，也可能不发生。
    2. 事件发生的可能性大小：
      • 判断方法： 可能性的大小与所包含的情况的数量有关，在所有情况中，某种情况占的比例越大，发生的可能性就越大。
      • 描述词语： “一定”、“不可能”、“可能”、“可能性大”、“可能性小”等。
    3. 游戏规则的公平性：
      • 判断标准： 游戏规则是否公平，取决于双方获胜的可能性是否相等。

第五单元：简易方程

本册书的难点和重点,是学生从算术思维向代数思维过渡的关键一步。

  • 核心知识点：

    1. 用字母表示数：

      • 意义： 用字母可以表示任意数、未知数、运算定律、计算公式等，具有概括性和简洁性。
      • 注意： 当字母与数字相乘时，省略乘号，并且把数字写在字母前面，a×5 写作 5a。
      • 平方： 2个a相乘 a×a 可以写作 a²，读作“a的平方”。

    2. 方程的意义：

      • 方程： 含有未知数的等式叫做方程。
      • 方程的必备条件： ①必须是等式；②必须含有未知数。
      • 等式的性质： 等式两边同时加上或减去同一个数，等式仍然成立；等式两边同时乘或除以同一个不为0的数，等式仍然成立，这是解方程的理论基础。

    3. 解方程：

      • 方法： 利用等式的性质，把方程转化成 x = a 的形式。
      • 检验： 把解得的x的值代入原方程，看左右两边是否相等。

    4. 列方程解决问题：

      • 步骤：
        1. 设未知数： 用字母（通常是x）表示未知数。
        2. 找等量关系： 根据题意，找出题目中数量之间的相等关系。
        3. 列方程： 把等量关系写成方程。
        4. 解方程： 求出未知数的值。
        5. 写答语： 检验并写出答案。
      • 关键： 找准等量关系是列方程解决问题的核心。

第六单元：多边形的面积

这是本学期的几何重点,通过“割补”、“平移”、“旋转”等方法，推导出常见图形的面积公式。

  • 核心知识点：

    1. 平行四边形的面积：

      • 公式： S = a × h (底 × 高)
      • 推导方法： 把平行四边形通过“割补”转化成一个长方形，长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高。

    2. 三角形的面积：

      • 公式： S = a × h ÷ 2 (底 × 高 ÷ 2)
      • 推导方法： 两个完全相同的三角形可以拼成一个平行四边形，这个平行四边形的底和高就是三角形的底和高，所以三角形的面积是平行四边形面积的一半。

    3. 梯形的面积：

      • 公式： S = (a + b) × h ÷ 2 (上底 + 下底) × 高 ÷ 2
      • 推导方法： 两个完全相同的梯形可以拼成一个平行四边形，这个平行四边形的底是梯形上底与下底之和，高就是梯形的高。

    4. 组合图形的面积：

      • 计算方法： 将组合图形分割成已学过的简单图形（长方形、正方形、平行四边形、三角形、梯形），分别计算出它们的面积，再相加。

第七单元：数学广角——植树问题

这是一个经典的数学模型问题,旨在培养学生的数学思维和解决问题的策略。

  • 核心知识点：
    • 三种情况：
      1. 两端都栽： 棵数 = 间隔数 + 1
      2. 一端栽，一端不栽： 棵数 = 间隔数
      3. 两端都不栽： 棵数 = 间隔数 - 1
    • 关键： 找到“棵数”与“间隔数”之间的关系，这个模型可以应用到生活中的很多问题，如安装路灯、锯木头、爬楼梯等。

第八单元：总复习

对本学期所有知识进行系统性的回顾、梳理和巩固，查漏补缺。

给家长和学生的学习建议

  1. 计算是基础： 小数乘除法是重中之重，一定要保证计算的准确性和速度，每天坚持做几道计算题，可以有效避免粗心。
  2. 理解重于记忆： 对于面积公式的推导过程，一定要理解其“转化”的思想，而不是死记硬背公式。
  3. 方程是难点： 学习方程时，要多练习“找等量关系”，可以尝试用画线段图的方式帮助理解，这是从算术思维到代数思维的巨大飞跃，需要多花时间适应。
  4. 联系生活实际： 数学来源于生活，也应用于生活，鼓励孩子用数学的眼光观察生活中的问题，比如购物、测量、规划等。
  5. 培养错题本习惯： 准备一个错题本，记录做错的题目和错误原因，定期复习，效果显著。

希望这份详细的梳理能帮助您更好地了解五年级上册的数学内容！