六年级上册数学课本有哪些重点难点？

小学六年级数学（上册）核心知识点总结

六年级上册的数学是整个小学阶段的重点和难点,内容多，综合性强，为初中数学学习打下坚实的基础，主要可以分为四大板块：分数乘法、分数除法、比和按比例分配、以及圆。

第一单元：分数乘法

这是本册的起点,也是后续学习分数除法和百分数的基础。

核心知识点：

1. 分数乘整数：

   • 意义： 求几个相同加数的和的简便运算。1/5 × 3 表示 3 个 1/5 相加。
   • 计算方法： 用分子和整数相乘的积作分子，分母不变，计算结果要化成最简分数。
   • 应用： 解决“求一个数的几分之几是多少”的问题。

2. 分数乘分数：

   • 意义： 求这个数的几分之几是多少。1/2 × 1/3 表示 1/2 的 1/3 是多少。
   • 计算方法： 用分子相乘的积作分子，分母相乘的积作分母，计算结果要化成最简分数。
   • 技巧： 计算过程中，可以先“约分”，再计算，使数字变小，计算更简便。

3. “求一个数的几分之几是多少”的应用题：

   
   （图片来源网络，侵删）
   • 这是本单元最重要的应用题类型。
   • 解题关键： 找到单位“1”（即标准量），然后用单位“1”的量 × 对应的分率 = 所求的量（分率对应的量）。
   • 例题： 一本书有 120 页，小明看了全书的 3/4，小明看了多少页？
     • 分析： 全书的页数是单位“1”，求看了多少页，就是求 120 的 3/4 是多少。
     • 列式： 120 × 3/4 = 90 (页)

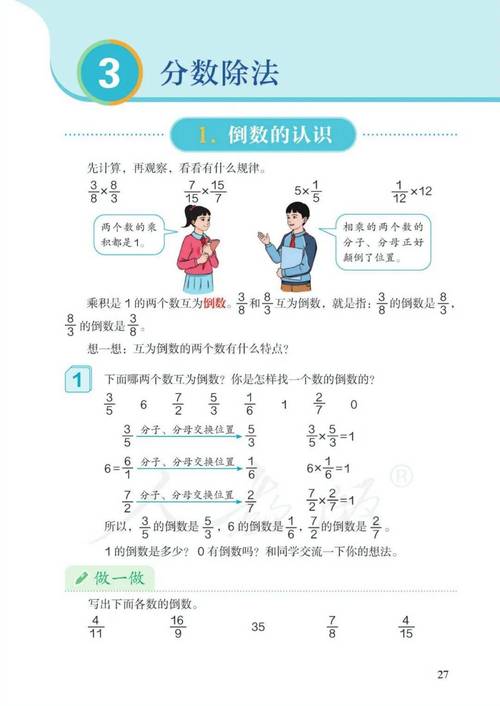
4. 倒数的认识：

   • 定义： 如果两个数的乘积是 1，那么这两个数互为倒数。
   • 求倒数的方法：
     • 真分数的倒数是假分数（如 3/4 的倒数是 4/3）。
     • 假分数的倒数是真分数或整数（如 5/2 的倒数是 2/5，7/1 的倒数是 1/7）。
     • 整数的倒数是 1 除以这个数（如 5 的倒数是 1/5）。
     • 1 的倒数是 1，0 没有倒数。

第二单元：分数除法

本单元是分数乘法的逆运算,是整个小学阶段的重点和难点。

核心知识点：

1. 分数除法的意义：

   • 与整数除法的意义相同,都是已知两个因数的积和其中一个因数，求另一个因数的运算。
   • 1/2 ÷ 1/4 表示已知一个数的 1/4 是 1/2，求这个数是多少。

2. 分数除法的计算法则：

   
   （图片来源网络，侵删）
   • 甲数除以乙数（0除外），等于甲数乘乙数的倒数。
   • 口诀： “除以一个数，等于乘这个数的倒数”。
   • 注意： 只有“除号”可以变成“乘号”，除数（第二个数）要变成它的倒数，分子和分母的位置不能随便交换。

3. “已知一个数的几分之几是多少，求这个数”的应用题：

   • 这是本单元最重要的应用题类型，也是难点。
   • 解题关键： 找到单位“1”（未知量），设单位“1”为 x，然后根据“单位‘1’ × 分率 = 分率对应的量”这个等量关系列出方程。
   • 例题： 一条裤子 75 元，是一件上衣价格的 3/5，上衣多少钱？
     • 分析： 上衣的价格是单位“1”，设为 x 元。
     • 列方程： x × 3/5 = 75
     • 解方程： x = 75 ÷ 3/5 = 75 × 5/3 = 125 (元)

4. 比的意义和基本性质：

   • 比的意义： 两个数相叉又比，表示两个数相除的关系，长是 3 米，宽是 2 米，长和宽的比是 3:2，宽和长的比是 2:3。
   • 比的基本性质： 比的前项和后项同时乘或除以相同的数（0除外），比值不变。
   • 化简比： 利用比的基本性质，把比化成最简单的整数比。12:18 = 2:3，4:0.6 = 4:6 = 2:3。
   • 求比值： 用比的前项除以后项。3:2 = 3 ÷ 2 = 1.5。

5. 按比例分配：

   • 应用题类型： 把一个量按照一定的比进行分配。
   • 解题步骤：
     1. 求总份数（比的前项和后项相加）。
     2. 求每份的量（总量 ÷ 总份数）。
     3. 求各部分的量（每份的量 × 各自的份数）。
   • 例题： 配制一种农药，药粉和水的比是 1:500，现在要配制 1002 千克的农药，需要药粉和水各多少千克？
     • 分析： 药粉:水 = 1:500，总份数是 1+500=501。
     • 计算：
       • 药粉：1002 × (1/501) = 2 (千克)
       • 水：1002 × (500/501) = 1000 (千克)

第三单元：圆

本单元是小学阶段最后学习的平面图形,引入了曲线图形，并首次接触有关圆周率π的计算。

核心知识点：

1. 圆的认识：

   • 圆心 (O)： 决定圆的位置。
   • 半径 (r)： 连接圆心和圆上任意一点的线段，决定圆的大小，在同一个圆里，半径有无数条，长度都相等。
   • 直径 (d)： 通过圆心并且两端都在圆上的线段，在同一个圆里，直径有无数条，长度都相等，且是半径的2倍 (d = 2r 或 r = d/2)。
   • 圆周率 (π)： 一个固定的数，约等于 3.1415926535...，小学阶段通常取 3.14。

2. 圆的周长：

   • 定义： 围成圆的曲线的长度。
   • 计算公式： C = πd 或 C = 2πr。
   • 应用： 已知直径或半径，求圆的周长。

3. 圆的面积：

   • 定义： 圆所占平面的大小。
   • 计算公式： S = πr² (r 是圆的半径)。
   • 重点： 推导过程是通过“化曲为直”、“化圆为方”的思想，将圆平均分成若干份，拼成一个近似的长方形，长方形的长相当于圆周长的一半 (πr)，宽相当于圆的半径。

4. 半圆的周长与面积：

   • 半圆的周长 (C半圆)： 不等于圆周长的一半，它还包括一条直径的长度。C半圆 = πr + 2r。
   • 半圆的面积 (S半圆)： 是圆面积的一半。S半圆 = πr² / 2。

第四单元：百分数

百分数是分数的另一种特殊形式,在生活中应用极其广泛。

核心知识点：

1. 百分数的意义： 表示一个数是另一个数的百分之几，它只能表示“分率”，不能表示一个具体的数量（后面不能带单位）。50% 米是错误的。

2. 百分数、分数、小数的互化：

   • 小数化百分数： 小数点向右移动两位，加上百分号。25 = 25%。
   • 百分数化小数： 小数点向左移动两位，去掉百分号。130% = 1.3。
   • 分数化百分数： 通常先把分数化成小数（除不尽时，通常保留三位小数），再化成百分数。3/4 = 0.75 = 75%。
   • 百分数化分数： 先把百分数改写成分母是100的分数，再化简。40% = 40/100 = 2/5。

3. 百分率的应用：

   • 常见类型： 出勤率、成活率、合格率、命中率、出油率等。
   • 通用公式： ×率 = (部分量 / 总量) × 100%。

4. “求一个数的百分之几是多少”的应用题：

   • 与分数乘法应用题完全相同。
   • 解题关键： 找到单位“1”，用单位“1”的量 × 百分率 = 所求的量。
   • 例题： 某工厂有工人 500 人，其中女工占 60%，女工有多少人？
     • 列式： 500 × 60% = 500 × 0.6 = 300 (人)

5. “已知一个数的百分之几是多少，求这个数”的应用题：

   • 与分数除法应用题完全相同。
   • 解题关键： 找到单位“1”（未知量），设为 x，列方程求解。
   • 例题： 一件衣服打八折后售价 160 元，原价是多少元？
     • 分析： 原价是单位“1”，设为 x 元，打折是“乘”，八折就是 × 80%。
     • 列方程： x × 80% = 160
     • 解方程： x = 160 ÷ 80% = 200 (元)

学习建议

1. 打好基础： 分数乘除法是重中之重，务必熟练掌握计算法则和“单位1”的判断方法。
2. 多画图： 学习分数应用题和圆的知识时，画线段图和示意图可以帮助理解题意，找到数量关系。
3. 勤于练习： 应用题的类型很多，要通过练习总结规律，特别是“求单位1”和“求分率对应的量”这两种基本题型。
4. 联系生活： 百分数、比、圆在生活中随处可见，多观察、多思考，能帮助理解抽象的数学概念。
5. 整理错题本： 把做错的题目抄下来，分析错误原因，定期复习，避免再犯同样的错误。

希望这份详细的总结能对您有所帮助！