整体概述
苏教版五年级下册的数学教材在知识体系上承上启下,是学生从整数运算向分数、小数等更复杂领域过渡的关键时期,本册内容注重培养学生的抽象思维能力、逻辑推理能力和解决实际问题的能力。

(图片来源网络,侵删)
全册教材主要分为以下几个大的单元:
- 方程:首次引入用字母表示数和方程的概念,是代数思维的启蒙。
- 因数与倍数:研究整数的性质,为后续学习分数约分、通分打下坚实基础。
- 分数的意义和性质:本册的绝对重点和难点,是分数概念的系统化学习。
- 分数的加法和减法:在理解分数意义的基础上,进行分数的运算。
- 圆:从直线图形过渡到曲线图形,学习圆的基本特征和周长、面积计算。
- 解决问题的策略:重点介绍“转化”这一重要的数学思想方法。
- 整理与复习:对本学期所有知识进行系统梳理和巩固。
各单元核心知识点详解
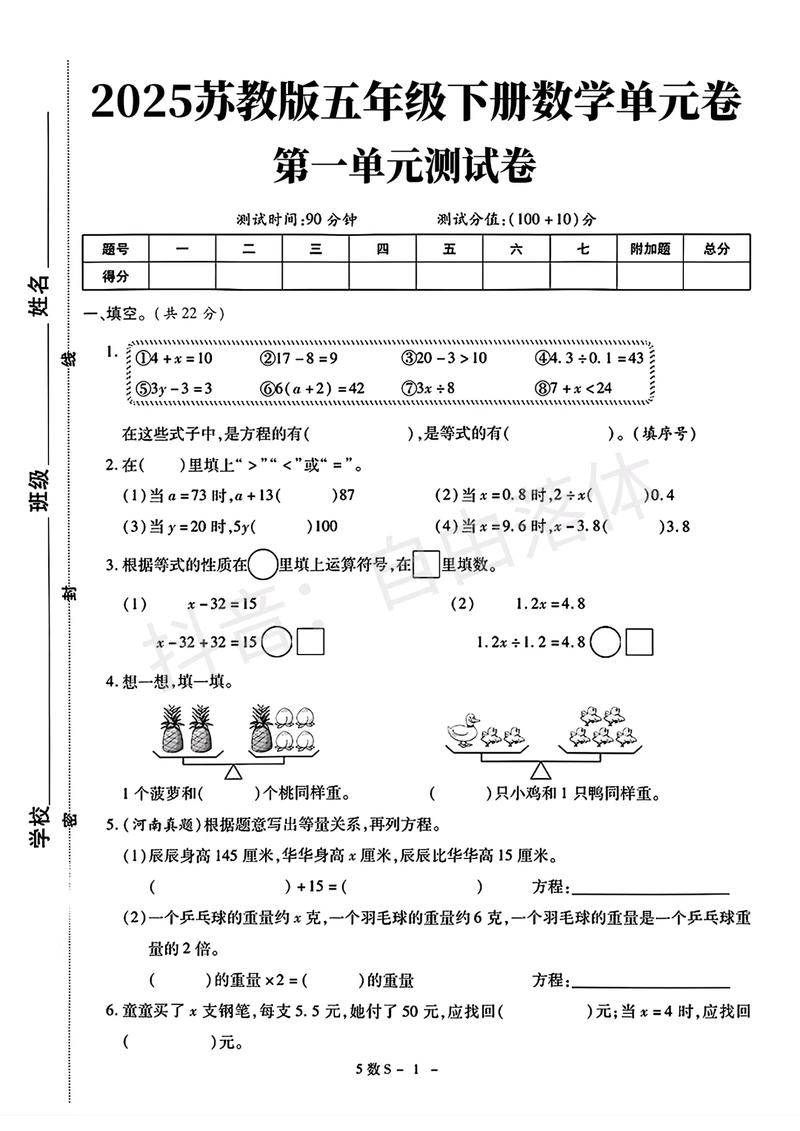
第一单元:方程
-
核心目标:用字母表示数,初步理解方程的意义,并学会解简单的方程。
-
重点知识点:
- 用字母表示数:
- 用字母表示数量关系(如:
S = a × b表示长方形的面积)。 - 用字母表示计算公式(如:
C = 2(a+b))。 - 含有字母的式子的简写规则(数字与字母相乘、字母与字母相乘、1与字母相乘的简写)。
- 用字母表示数量关系(如:
- 等式与方程:
- 等式:表示两边相等的式子(如
3+5=8,10÷2=5)。 - 方程:含有未知数的等式。关键特征:① 必须是等式;② 必须含有未知数。
- 判断一个式子是不是方程。
- 等式:表示两边相等的式子(如
- 等式的性质:
- 性质1:等式两边同时加上或减去同一个数,所得结果仍然是等式。(这是解方程的基础)
- 性质2:等式两边同时乘或除以同一个不为0的数,所得结果仍然是等式。
- 解方程:
- 根据等式的性质,求出方程中未知数的值。
- 格式要求:解、写“解”、等号对齐。
- 列方程解决实际问题:
- 关键步骤:① 弄清题意,找出未知量,用字母表示;② 找出等量关系;③ 列出方程;④ 解方程;⑤ 检验并作答。
- 常见的等量关系:和、差、倍数关系,以及行程、工程等基本问题。
- 用字母表示数:
-
常见难点:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 对“方程”概念的理解,区分方程和等式。
- 在复杂问题中找准等量关系。
- 解形如
a - x = b或ax - b = c的方程。
第二单元:因数与倍数
-
核心目标:理解因数、倍数的意义,掌握2、5、3的倍数的特征,认识质数和合数。
-
重点知识点:
- 因数和倍数:
a ÷ b = c(且c是整数),a是b的倍数,b是a的因数。- 注意:因数和倍数是相互依存的,不能单独说某个数是因数或倍数,研究范围是非0自然数。
- 找一个数的因数和倍数:
- 找因数:成对找,从1开始,一对一对地找,直到两个数接近或相等,一个数的因数是有限的,其中最小的因数是1,最大的因数是它本身。
- 找倍数:用这个数分别乘1、2、3、4… 一个数的倍数是无限的,最小的倍数是它本身,没有最大的倍数。
- 2、5、3的倍数的特征:
- 2的倍数:个位上是0、2、4、6、8的数。特征:是偶数。
- 5的倍数:个位上是0或5的数。
- 3的倍数:各位上数字的和是3的倍数。
- 质数与合数:
- 质数(素数):只有1和它本身两个因数。(如:2, 3, 5, 7, 11...)
- 合数:除了1和它本身,还有其他因数。(如:4, 6, 8, 9, 10...)
- 1:既不是质数,也不是合数。
- 100以内的质数表:要求熟记。
- 因数和倍数:
-
常见难点:
- 概念易混淆,如因数和倍数的关系,质数和奇数、合数和偶数的关系(2是唯一的偶质数)。
- 综合运用多种特征解决问题(如:同时是2、3、5的倍数的数的特征)。
第三单元:分数的意义和性质
-
核心目标:深刻理解分数的意义,掌握分数的基本性质,并能进行分数的互化和大小比较。
 (图片来源网络,侵删)
(图片来源网络,侵删) -
重点知识点:
- 分数的意义:
- 把单位“1”平均分成若干份,表示这样的一份或几份的数,叫做分数。
- 单位“1”:不仅可以是一个物体,也可以是一堆物体、一个整体。
- 分数与除法的关系:
- 被除数 ÷ 除数 = 被除数 / 除数 (
a ÷ b = a/b,b≠0) - 分数的分子相当于被除数,分母相当于除数。
- 被除数 ÷ 除数 = 被除数 / 除数 (
- 真分数和假分数:
- 真分数:分子小于分母,分数值小于1。
- 假分数:分子大于或等于分母,分数值大于或等于1。
- 带分数:由整数部分和真分数部分组成(如
1 1/2)。 - 假分数与带分数的互化。
- 分数的基本性质:
- 分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
- 核心作用:是约分和通分的理论依据。
- 约分和通分:
- 约分:把一个分数化成和它相等,但分子、分母都比较小的分数,通常要约成最简分数(分子分母互质)。
- 通分:把几个异分母分数分别化成和原来分数相等的同分母分数,通常用这几个分母的最小公倍数作公分母。
- 分数的大小比较:
- 同分母分数:分子大的分数大。
- 同分子分数:分母小的分数大。
- 异分母分数:先通分,再按同分母分数比较大小。
- 分数的意义:
-
常见难点:
- 对“单位1”和“分数意义”的抽象理解。
- 约分和通分的熟练掌握,尤其是找最大公因数和最小公倍数。
- 假分数与带分数、整数之间的互化。
第四单元:分数的加法和减法
-
核心目标:掌握分数加减法的计算法则,并能解决实际问题。
-
重点知识点:
- 同分母分数加减法:
- 法则:分母不变,分子相加减。
- 计算结果能约分的要约分,是假分数的要化成带分数或整数。
- 异分母分数加减法:
- 法则:先通分,化成同分母分数,再按照同分母分数加减法计算。
- 关键:通分是前提。
- 分数加减法的混合运算:
- 运算顺序与整数相同:有括号的先算括号里的,没有括号的从左到右依次计算。
- 整律加法交换律、结合律在分数运算中同样适用。
- 分数加减法的简便运算:
- 运用运算定律进行简算,如
1/2 + 1/4 + 1/8 + 1/8可以用加法交换律和结合律。
- 运用运算定律进行简算,如
- 同分母分数加减法:
-
常见难点:
- 异分母分数加减法中,通分容易出错。
- 计算结果忘记化成最简形式。
- 混合运算中,运算顺序的把握和定律的灵活运用。
第五单元:圆
-
核心目标:认识圆,掌握圆的周长和面积的计算公式,并能解决相关问题。
-
重点知识点:
- 圆的认识:
- 圆心 (O):决定圆的位置。
- 半径:连接圆心和圆上任意一点的线段,在同一个圆里,半径有无数条,长度都相等。
- 直径:通过圆心并且两端都在圆上的线段,在同一个圆里,直径有无数条,长度都相等。
d = 2r。
- 圆的周长:
- 围成圆的曲线的长叫做周长。
- 圆周率 (π):任意一个圆的周长与它的直径的比值是一个固定的数,它是一个无限不循环小数,约等于3.14159... 在小学阶段,通常取
π ≈ 3.14。 - 周长公式:
C = πd或C = 2πr。
- 圆的面积:
- 圆所占平面的大小叫做面积。
- 面积公式:
S = πr²(r是圆的半径)。 - 推导思想:“化曲为直”、“化圆为方”,通过将圆分割成若干等份,拼成一个近似的长方形来推导。
- 半圆的周长与面积:
- 半圆的周长 = 圆周长的一半 + 直长 (
C半 = πr + 2r)。 - 半圆的面积 = 圆面积的一半 (
S半 = πr² ÷ 2)。
- 半圆的周长 = 圆周长的一半 + 直长 (
- 圆的认识:
-
常见难点:
- 对 的理解和取值。
- 区分周长和面积,以及对应的公式。
- 解决组合图形(如:正方形内最大的圆,圆内最大的正方形)的周长和面积问题。
第六单元:解决问题的策略——转化
- 核心目标:体验“转化”这一策略的价值,学会用转化的思想方法解决一些实际问题。
- 重点知识点:
- 什么是转化:把未知的问题、复杂的问题,变成已知的问题、简单的问题来解决。
- 应用场景:
- 计算不规则图形的面积时,可以通过平移、旋转、割补等方法,将其转化为规则图形(如长方形、正方形)来计算。
- 计算分数加减法时,通分就是将异分母分数转化为同分母分数。
- 本单元重点:通过计算图形的周长和面积,体会“转化”策略的妙用。
学习建议
- 注重概念理解:特别是“方程”、“分数的意义”、“圆”等单元,不能只记公式,要真正理解其内涵。
- 强化计算能力:分数的运算是基础,要通过大量练习做到准确、迅速。
- 培养画图习惯:在学习“圆”和“解决问题”时,画图能帮助理解题意,找到解题思路。
- 建立知识联系:将各单元知识点串联起来,如“因数倍数”为“分数”服务,“分数”又为“解决问题”服务,形成一个知识网络。
- 多做错题整理:准备一个错题本,分析错误原因,定期回顾,避免重复犯错。
- 联系生活实际:数学源于生活,鼓励孩子发现生活中的数学问题,并用所学知识去解决。
希望这份详细的梳理对您有所帮助!


