负数、圆柱与圆锥、以及比例,还有“数学广角”和“总复习”。

(图片来源网络,侵删)
第一单元:负数
这是小学阶段首次引入“有理数”的初步概念,是数域的一次重要扩展。
核心知识点:
-
负数的意义:
- 定义: 为了表示与具有相反意义的量,我们引入了负数,像 -3, -1/2, -0.5 这样的数叫做负数。
- “0”的意义: 0既不是正数,也不是负数,它是正数和负数的分界点。
- 生活中的应用: 温度计(0℃以上为正,以下为负)、海拔高度(海平面以上为正,以下为负)、收入与支出、盈利与亏损等。
-
用正负数表示相反意义的量:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 关键在于找到一个“标准”或“基准”(通常记为0),然后用正数和负数来描述与这个基准相反的两个方向的量。
- 如果向东走50米记作 +50米,那么向西走50米就记作 -50米。
-
在数轴上表示数:
- 数轴的三要素: 原点、正方向、单位长度。
- 如何表示:
- 所有正数都在0的右边,所有负数都在0的左边。
- 在数轴上,右边的数总比左边的数大。
- 0左边的数都是负数,离0越远,这个负数越小(-5 < -3)。
学习要点:
- 重点理解负数的实际意义,而不是死记硬背符号。
- 能够熟练地将具体情境中的量用正负数表示出来。
- 掌握在数轴上比较数的大小,尤其是负数之间、负数与正数之间的大小比较。
第二单元:圆柱与圆锥
这是对小学阶段所学的“立体图形”知识的拓展和深化,重点学习两种新的旋转体。
核心知识点:
(图片来源网络,侵删)
圆柱
-
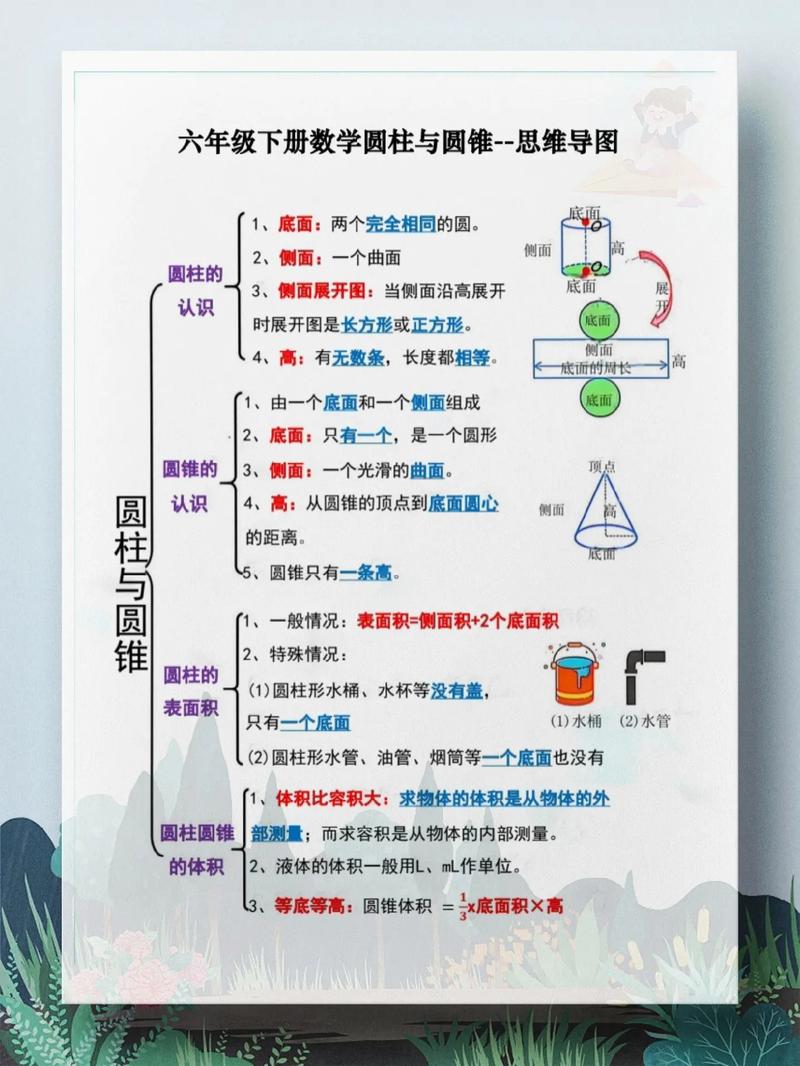
圆柱的认识:
- 特征: 由两个完全相同的圆形底面和一个曲面侧面组成。
- 高: 两个底面之间的距离,有无数条高,长度都相等。
-
圆柱的表面积:
- 侧面积: 将圆柱侧面沿高展开,得到一个长方形,长方形的长等于圆柱底面的周长(C = πd 或 C = 2πr),长方形的宽等于圆柱的高。
- 侧面积公式:
S侧 = Ch = πdh = 2πrh - 表面积公式:
S表 = S侧 + 2S底 = Ch + 2πr² = 2πrh + 2πr²
-
圆柱的体积:
- 公式:
V = Sh(底面积 × 高) - 推导: 将圆柱“切拼”成一个近似的长方体,这个长方体的体积与圆柱相等,长方体的底面积等于圆柱的底面积,高等于圆柱的高。
- 具体公式:
V = πr²h
- 公式:
圆锥
-
圆锥的认识:
- 特征: 由一个圆形底面和一个顶点,以及连接顶点和底面圆周上所有点的曲面侧面组成。
- 高: 从顶点到底面圆心的垂直距离,圆锥只有一条高。
-
圆锥的体积:
- 公式:
V = (1/3)Sh(底面积 × 高 ÷ 3) - 推导(关键!): 通过等底等高的圆柱和圆锥倒水(或沙子)的实验,发现圆锥的体积是圆柱体积的三分之一。
- 核心结论: 等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍,圆锥的体积是圆柱的1/3。
- 具体公式:
V = (1/3)πr²h
- 公式:
学习要点:
- 空间观念: 动手操作(制作模型、切拼)是建立空间观念的最好方法。
- 公式的理解与记忆: 理解每个公式的推导过程,而不是死记硬背,特别是圆锥体积公式的“1/3”。
- 单位换算: 计算表面积和体积时,要特别注意单位的统一(长度单位、面积单位、体积单位)。
- 实际问题: 能运用公式解决求水桶用料(表面积)、粮仓容积(体积)、压路机滚筒压过的面积(侧面积)等实际问题。
第三单元:比例
是小学数学的重点和难点,它用一种新的函数关系来描述数量之间的联系,为学习初中函数打下基础。
核心知识点:
-
比例的意义和基本性质:
- 比例: 表示两个比相等的式子叫做比例,如
a : b = c : d。 - 比例的基本性质: 在比例里,两个外项的积等于两个内项的积(
ad = bc),这是解比例的依据。
- 比例: 表示两个比相等的式子叫做比例,如
-
正比例和反比例:
- 正比例:
- 关系: 两种相关联的量,一种量变化,另一种量也随着变化,且它们的比值(商)一定。
- 关系式:
y/x = k (一定)或y = kx(k是定值)。 - 图像: 一条过原点的直线。
- 反比例:
- 关系: 两种相关联的量,一种量变化,另一种量也随着变化,且它们的积一定。
- 关系式:
xy = k (一定)或y = k/x(k是定值)。 - 图像: 一条双曲线(小学阶段不要求画图,但要理解其趋势)。
- 判断方法: 找出两种相关联的量,看它们的比值是否一定(正比例),还是积是否一定(反比例)。
- 正比例:
-
比例尺:
- 意义: 图上距离与实际距离的比。
- 公式:
比例尺 = 图上距离 : 实际距离 - 表示形式: 数值比例尺(如 1:5000000)和线段比例尺。
- 计算: 灵活运用公式进行“图上距离”、“实际距离”和“比例尺”三者之间的换算,注意单位的统一。
-
用比例解决问题:
- 关键步骤:
- 判断比例关系: 首先判断题目中的两种量是成正比例还是成反比例关系。
- 设未知数: 设要求的量为x。
- 列等式(比例式): 根据比例关系列出等式。
- 正比例:
第一个量的比 = 第二个量的比 - 反比例:
第一个量的积 = 第二个量的积
- 正比例:
- 解比例并作答。
- 关键步骤:
学习要点:
- 核心是“关系”: 比例的本质是研究数量之间的一种特殊关系。
- 辨析正反比例: 这是难点,要通过大量练习,掌握判断方法,抓住“比值一定”还是“积一定”这个核心。
- 比例尺的应用: 与生活实际联系紧密,要能看懂地图、设计图纸等。
- 解比例的技能: 熟练运用比例的基本性质解比例方程。
第四单元:数学广角——鸽巢问题
属于奥数范畴,主要训练学生的逻辑思维和模型思想。
核心知识点:
-
鸽巢原理(抽屉原理):
- 最简单形式: 只要把更多的苹果放入较少的抽屉中,那么至少有一个抽屉里有两个或更多的苹果。
- 模型: 物体(鸽子) -> 抽屉(鸽巢)。
- 核心结论: 只要将
n+1个物体放入n个抽屉中,那么至少有一个抽屉里放有2个物体。
-
原理的推广:
- 把
m个物体任意放进n个抽屉里(m > n),那么至少有一个抽屉里放有 ⌈m/n⌉ 个物体。(⌈ ⌉表示向上取整) - 例子: 把 5 个苹果放进 2 个抽屉,至少有一个抽屉里有
⌈5/2⌉ = 3个苹果。
- 把
学习要点:
- 建立模型: 关键在于分析问题,判断谁是“物体”,谁是“抽屉”。
- 逆向思维: 这类问题常常需要从“保证”或“至少”的角度去思考,是一种逆向思维训练。
- 解决策略: 通常使用“假设法”,即假设每个抽屉放的物体尽可能平均,然后根据总数来推算。
第五单元:总复习
这是对整个小学阶段(1-6年级)所有数学知识的系统性回顾、梳理和巩固。
复习策略:
-
分模块复习:
- “数与代数”: 整数、小数、分数、百分数的意义、性质和运算;比和比例;方程等。
- “图形与几何”: 平面图形(周长、面积)、立体图形(表面积、体积)、图形的位置与变换(平移、旋转、轴对称)。
- “统计与概率”: 数据的收集、整理与表示(条形、折线、扇形统计图);可能性的大小。
- “综合与实践”: 解决问题的策略,如列表、画图、假设、转化等。
-
构建知识网络: 将零散的知识点串联起来,形成知识体系,长方形面积、平行四边形面积、三角形面积、梯形面积、圆面积之间的联系。
-
查漏补缺: 针对自己薄弱的环节进行专项练习。
-
综合应用: 解决复杂的、多步骤的实际问题,提高综合运用知识的能力。
学习建议
- 回归课本,夯实基础: 所有的难题都源于基本概念和公式,确保对每个知识点都有清晰的理解。
- 勤于思考,多问“为什么”: 不要满足于会做题,要理解公式背后的原理和推导过程。
- 建立错题本: 记录错题,分析错误原因,定期回顾,避免重复犯错。
- 联系生活,学以致用: 将数学知识与生活中的问题联系起来,感受数学的价值和趣味。
- 保持良好心态: 六年级下册内容有一定难度,遇到困难是正常的,保持积极心态,多与老师同学交流。
希望这份知识点梳理能帮助您更好地把握六年级下册的数学学习!


