三年级上册数学核心知识点有哪些？

第一单元：时、分、秒

这是本册书的新增内容,重点是建立时间观念。

1. 认识时间单位

   • 单位： 时、分、秒。
   • 关系： 1时 = 60分，1分 = 60秒。
   • 进率： 时、分、秒之间的进率是60。

2. 时间的计算

   • 计算“经过时间”： 知道开始时刻和结束时刻，求中间经过了多长时间。
     • 方法1： 数一数（适合简单的、时间跨度小的）。
     • 方法2： 结束时刻 - 开始时刻 = 经过时间。
   • 计算“结束时刻”： 开始时刻 + 经过时间 = 结束时刻。
   • 计算“开始时刻”： 结束时刻 - 经过时间 = 开始时刻。

3. 时间单位的简单换算

   • 把较大的单位换算成较小的单位，用乘法（如：2时 = 2 × 60 = 120分）。
   • 把较小的单位换算成较大的单位，用除法（如：180秒 = 180 ÷ 60 = 3分）。

第二单元：万以内的加法和减法（一）

是在100以内加减法基础上的扩展,重点是掌握口算和估算。

1. 两位数加两位数的口算

   • 方法： 把其中一个加数拆成整十数和一位数，再分步相加。
     • 例：35 + 47 = 35 + 40 + 7 = 75 + 7 = 82
     • 例：35 + 47 = 30 + 40 + 5 + 7 = 70 + 12 = 82

2. 两位数减两位数的口算

   • 方法： 把减数拆成整十数和一位数，再分步相减。
     • 例：83 - 57 = 83 - 50 - 7 = 33 - 7 = 26

3. 几百几十加减几百几十的笔算

   • 方法： 与两位数加减两位数的笔算方法相同，注意相同数位对齐,从个位算起。
   • 注意： 满十要向前一位进一,不够减要向前一位借一当十。

4. 估算

   
   （图片来源网络，侵删）
   • 目的： 不需要计算出精确结果,用来检验计算结果的大致范围或快速解决问题。
   • 方法： 把加数、被减数、减数都看作与它接近的整百数或整十数，再进行计算。
     • 例：398 + 204 ≈ 400 + 200 = 600
     • 例：803 - 596 ≈ 800 - 600 = 200

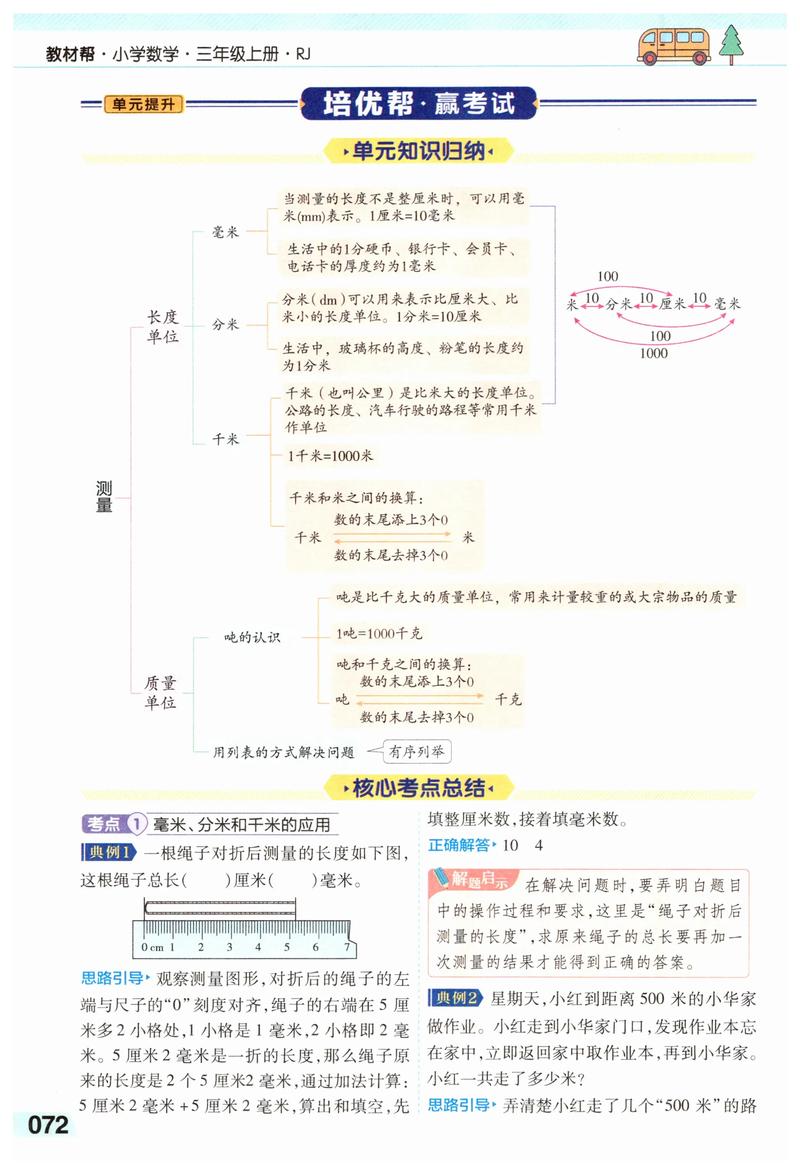
第三单元：测量

本单元是另一个重点和难点,孩子们需要建立长度单位和质量单位的观念。

1. 长度单位

   • 单位： 毫米、厘米、分米、米、千米。
   • 关系与进率：
     • 1厘米 = 10毫米
     • 1分米 = 10厘米 = 100毫米
     • 1米 = 10分米 = 100厘米 = 1000毫米
     • 1千米 = 1000米 (千米也叫“公里”)
   • 建立观念：
     • 毫米： 1分硬币的厚度大约是1毫米。
     • 千米： 运动场的跑道一圈通常是400米，两半圈就是1千米,感受1千米有多远。
   • 长度单位的换算： 与时间单位换算类似，大化小乘以进率,小化大除以进率。

2. 质量单位

   • 单位： 吨、千克、克。
   • 关系与进率：
     • 1千克 = 1000克
     • 1吨 = 1000千克
   • 建立观念：
     • 克： 一枚2分硬币大约重1克。
     • 千克： 一包方便面、两瓶矿泉水大约重1千克。
     • 吨： 一头大象、一辆小汽车的重量大约是1吨或几吨,吨是用来计量很重的物品的。
   • 质量单位的换算： 同样遵循大化小乘,小化大除的原则。

第四单元：万以内的加法和减法（二）

这是笔算加减法的综合运用,涉及到连续进位和连续退位。

1. 三位数加三位数（笔算）

   • 法则：
     • 相同数位对齐。
     • 从个位加起。
     • 哪一位上的数相加满十,就要向前一位进一。
   • 重点： 连续进位（个位满十向十位进一，十位满十又要向百位进一）。

2. 三位数减三位数（笔算）

   • 法则：
     • 相同数位对齐。
     • 从个位减起。
     • 哪一位上的数不够减，就要从前一位退一当十,和本位上的数合起来再减。
   • 重点： 连续退位（个位不够减，向十位借一，如果十位是0，就需要继续向百位借）。

3. 解决问题

   • “求比一个数多几或少几的数是多少”的应用题。
     • 求比一个数多几的数用加法。
     • 求比一个数少几的数用减法。

第五单元：倍的认识

这是本册书的一个重要概念，是后续学习分数、除法等知识的基础。

1. 倍的意义

   • 定义： 一个数里面有几个另一个数,就说这个数是另一个数的几倍。
   • 关系： 倍数 = 几倍数 ÷ 1倍数
   • 解题关键： 找准“1倍数”是谁（也就是“标准量”）。

2. 解决“求一个数是另一个数的几倍”的问题

   • 方法： 用除法计算。
     • 例：苹果有12个，梨有3个,苹果的个数是梨的几倍？
     • 解：12 ÷ 3 = 4

3. 解决“求一个数的几倍是多少”的问题

   • 方法： 用乘法计算。
     • 例：梨有3个，苹果的个数是梨的4倍,苹果有多少个？
     • 解：3 × 4 = 12

第六单元：多位数乘一位数

这是本册书的计算重点,是整个小学阶段乘法的基础。

1. 口算乘法

   • 整十、整百数乘一位数： 先把0前面的数相乘，再看因数末尾有几个0，就在积的末尾添上几个0。

     例：20 × 3 = 60， 200 × 3 = 600

2. 笔算乘法

   • 不进位的乘法： 从个位乘起，用一位数依次去乘多位数的每一位，乘到哪一位,积就写在哪一位的下面。
   • 进位的乘法： 哪一位乘得的积满几十,就要向前一位进几。
   • 连续进位的乘法： 注意每一位的进位,不要漏掉。
   • 一个因数中间有0的乘法： 0和任何数相乘都得0。
   • 一个因数末尾有0的乘法： 可以先用0前面的数相乘，再看因数末尾有几个0，就在积的末尾添上几个0。（简便方法）

第七单元：长方形和正方形

这是本册书的几何部分,重点在于图形的特征和周长的计算。

1. 四边形

   • 特征： 由四条线段围成的封闭图形（有4个角，4条边）。

2. 长方形和正方形的特征

   • 长方形： 对边相等,4个角都是直角。
   • 正方形： 4条边都相等，4个角都是直角。（正方形是特殊的长方形）

3. 周长

   • 定义： 封闭图形一周的长度,就是它的周长。
   • 长方形的周长计算公式：
     • 方法1（加法）： 长 + 宽 + 长 + 宽
     • 方法2（简便）： (长 + 宽) × 2
   • 正方形的周长计算公式：
     • 方法1（加法）： 边长 + 边长 + 边长 + 边长
     • 方法2（简便）： 边长 × 4

4. 解决实际问题

   • 不规则图形的周长： 可以通过平移、拼接等方法,把它转化成一个长方形或正方形来计算周长。
   • “已知周长求边长”的问题： 用周长除以相应的份数。
     • 例：一个正方形的周长是20厘米,它的边长是多少？
     • 解：20 ÷ 4 = 5 (厘米)

第八单元：分数的初步认识

这是分数学习的入门,重点是理解分数的意义。

1. 分数的初步认识

   • 意义： 把一个整体平均分成几份，这样的1份就是它的几分之一,其中的几份就是它的几分之几。
   • 关键： “平均分” 是分数产生的前提。
   • 各部分名称：
     • 分数线
     • 3：分子（表示取的份数）
     • 4：分母（表示平均分成的份数）

2. 分数的简单计算

   • 同分母分数加法： 分母不变，分子相加。
     • 例：1/4 + 2/4 = 3/4
   • 同分母分数减法： 分母不变，分子相减。
     • 例：5/6 - 2/6 = 3/6
   • 1减几分之几： 把1写成与减数分母相同的分数，再相减。
     • 例：1 - 3/8 = 8/8 - 3/8 = 5/8

3. 分数的简单应用

   • 求一个数的几分之几是多少： 用乘法（这个内容在三年级下册会更深入，这里初步接触）。
   • 解决实际问题： 结合具体情境,理解分数的含义。

学习建议

• 计算是基础： 每天坚持5-10分钟的口算或笔算练习,提高计算的准确率和速度。
• 概念要吃透： 对于“倍”、“周长”、“分数”等核心概念，要结合实物和生活实例帮助孩子理解,而不是死记硬背公式。
• 多动手操作： 在学习“测量”、“图形”等单元时，多让孩子动手量一量、画一画、拼一拼,建立直观的印象。
• 联系生活实际： 引导孩子发现生活中的数学问题，比如购物算账、看时间、测量家具长度等，让数学“活”起来。
• 重视错题： 准备一个错题本，分析错误原因，定期回顾,避免重复犯错。

希望这份详细的知识点总结对您和孩子有所帮助！