整体概览

五年级下册的数学内容在难度上有了显著提升，开始引入更抽象的数学概念，如方程和因数与倍数，同时加强了空间与图形部分的知识,整个学期的学习可以大致分为四个模块：

小学五年级下册数学书苏教版
（图片来源网络，侵删）
  1. 数与代数：方程、因数与倍数、分数的意义和性质。
  2. 图形与几何：圆的周长与面积。
  3. 统计与概率：复式折线统计图。
  4. 实践与综合应用：解决问题的策略（转化）。

各单元核心知识点

以下是各单元的重点、难点和学习建议：

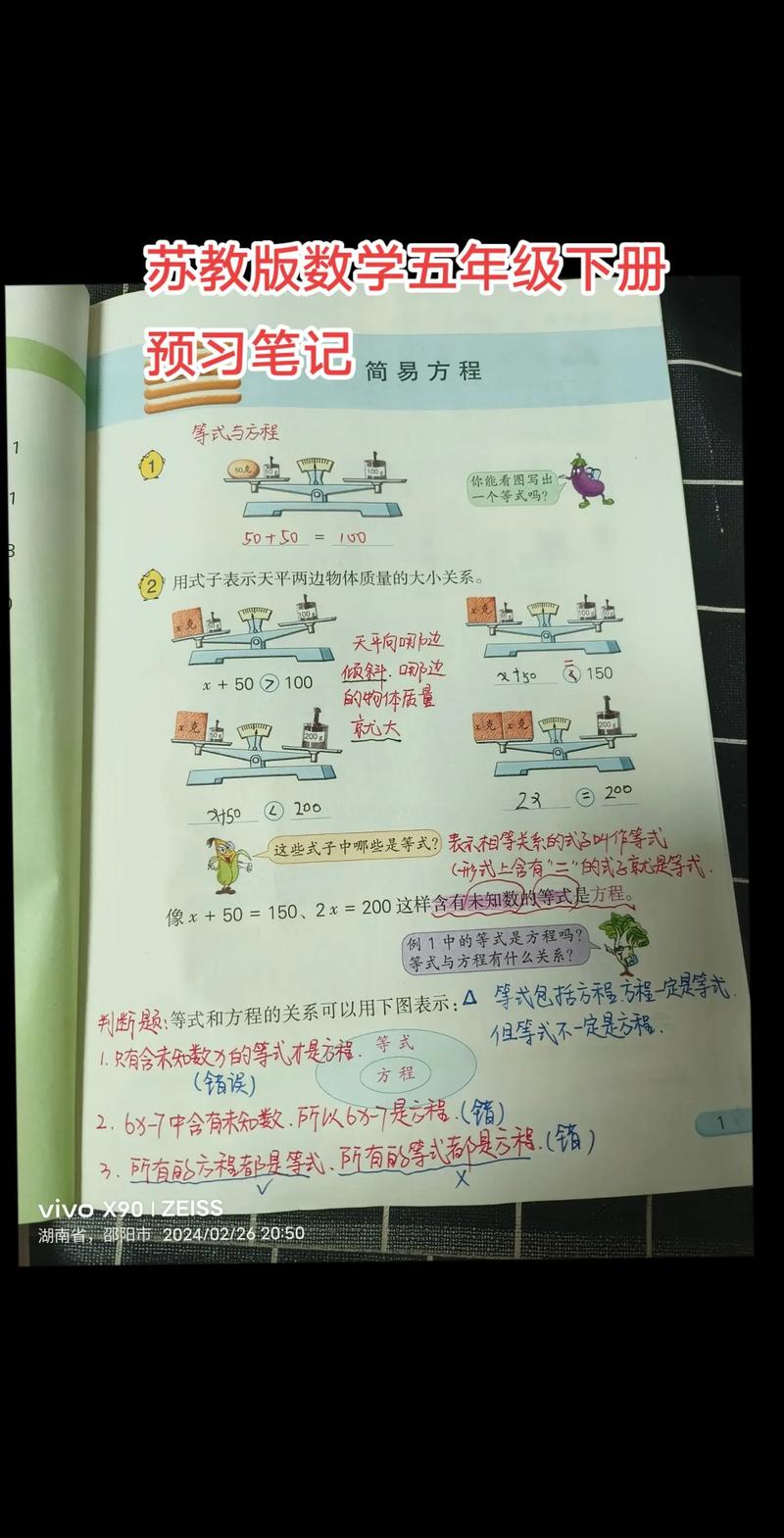
第一单元：简易方程

这是本学期的重点和难点,是学生从算术思维迈向代数思维的关键一步。

  • ：
    1. 方程的意义：理解“含有未知数的等式是方程”。
    2. 等式的性质：
      • 性质1：等式两边同时加上或减去同一个数,所得结果仍然是等式。
      • 性质2：等式两边同时乘或除以同一个不为0的数，所得结果仍然是等式。（这是解方程的理论基础）
    3. 解方程：利用等式的性质求出方程中未知数的值。
    4. 列方程解决实际问题：
      • 关键是找等量关系。
      • 步骤：设未知数 → 找等量关系 → 列方程 → 解方程 → 检验并作答。
  • 学习重点与难点：
    • 重点：理解方程的概念,掌握解方程的方法。
    • 难点：寻找实际问题中的等量关系，特别是涉及两个未知量的问题（和差问题、和倍问题、差倍问题）。
  • 学习建议：
    • 多动手练习解方程,确保步骤规范。
    • 对于应用题，不要急于列式，先反复读题,用画线段图或列表格的方式帮助分析数量关系。
    • 养成检验的好习惯，将解得的答案代入原题,看是否符合题意。

第二单元：因数与倍数

非常抽象，概念多且容易混淆,需要学生在理解的基础上进行记忆和区分。

  • ：
    1. 因数和倍数：a × b = c，a 和 b 是 c 的因数，c 是 a 和 b 的倍数。
    2. 2、5、3的倍数的特征：
      • 2的倍数：个位上是0、2、4、6、8的数。
      • 5的倍数：个位上是0或5的数。
      • 3的倍数：各位上数字的和是3的倍数。
    3. 质数和合数：
      • 质数（素数）：只有1和它本身两个因数。（如2, 3, 5, 7...）
      • 合数：除了1和它本身，还有其他因数。（如4, 6, 8, 9...）
      • 1：既不是质数,也不是合数。
    4. 最大公因数和最小公倍数：
      • 公因数和最大公因数。
      • 公倍数和最小公倍数。
      • 短除法：是求最大公因数和最小公倍数的重要方法。
  • 学习重点与难点：
    • 重点：掌握2、5、3的倍数的特征,理解质数和合数的概念。
    • 难点：区分质数与奇数、合数与偶数；熟练运用短除法求最大公因数和最小公倍数。
  • 学习建议：
    • 制作概念卡片，帮助区分易混淆的知识点（如因数和倍数的关系，质数与合数的区别）。
    • 通过列举具体数字来验证规律,加深理解。
    • 熟练掌握短除法，这是解决相关计算问题的“利器”。

第三单元：分数的意义和性质

是分数学习的深化和系统化,为后续学习分数运算打下坚实基础。

小学五年级下册数学书苏教版
（图片来源网络，侵删）
  • ：
    1. 分数的意义：把单位“1”平均分成若干份,表示这样的一份或几份的数。
    2. 分数与除法的关系：被除数 ÷ 除数 = 被除数 / 除数 (除数 ≠ 0)。
    3. 真分数和假分数：
      • 真分数：分子小于分母,小于1。
      • 假分数：分子大于或等于分母，大于或等于1,假分数可以化成整数或带分数。
    4. 分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。（这是约分和通分的依据）
    5. 约分和通分：
      • 约分：利用分数的基本性质,把分数化成最简分数。
      • 通分：利用分数的基本性质，把几个分数化成分母相同（但不一定是最小公倍数）的分数。
    6. 分数的大小比较：同分母分数直接比分子，同分子分数比分母,异分母分数先通分再比较。
  • 学习重点与难点：
    • 重点：理解分数的意义，掌握分数的基本性质,并能熟练进行约分和通分。
    • 难点：理解单位“1”的抽象性,灵活运用分数的基本性质解决实际问题。
  • 学习建议：
    • 多借助图形（如长方形、圆形）来表示分数,帮助建立直观感受。
    • 牢记“分子相当于被除数，分母相当于除数”，以及“分数的基本性质”的核心是“和“相同”。
    • 约分要彻底（分子分母互质），通分要准确（找到最小公倍数）。

第四单元：分数的加法和减法

  • ：
    1. 同分母分数加、减法：分母不变,分子相加减。
    2. 异分母分数加、减法：先通分，化成同分母分数,再计算。
    3. 分数加减混合运算：
      • 运算顺序与整数相同。
      • 可以一次性通分,也可以分步计算。
  • 学习重点与难点：
    • 重点：掌握异分母分数加减法的计算方法。
    • 难点：计算结果的化简（约分）,以及解决涉及分数加减法的实际问题。
  • 学习建议：
    • 计算时一定要细心，通分是关键一步,不要出错。
    • 计算结果能约分的要约成最简分数,是假分数的要化成带分数。
    • 多做混合运算练习,注意运算符号和括号。

第五单元：圆

这是本学期图形部分的核心，从直线图形（长方形、正方形）过渡到曲线图形（圆）。

  • ：
    1. 圆的认识：圆心、半径、直径及其关系（d=2r）。
    2. 圆的周长：
      • 公式：C = πd 或 C = 2πr (π ≈ 3.14)。
      • 理解圆周率π的意义。
    3. 圆的面积：
      • 公式：S = πr²。
      • 推导过程：通过“化曲为直”、“化圆为方”的思想,将圆转化成一个近似的长方形来推导。
    4. 半圆的周长与面积：半圆的周长 = πr + 2r，半圆的面积 = πr² / 2。
  • 学习重点与难点：
    • 重点：掌握圆的周长和面积的计算公式。
    • 难点：理解圆面积公式的推导过程，区分“周长”和“面积”,解决组合图形的周长和面积问题。
  • 学习建议：
    • 动手操作，用线绕一绕圆的周长，用数方格的方式感受圆的面积,帮助理解。
    • 记牢公式，并理解每个字母的含义（r是半径，d是直径）。
    • 解决问题时，要先看清题目要求的是周长还是面积,再选择正确的公式。

第六单元：解决问题的策略——转化

这是一个重要的数学思想方法,贯穿于整个数学学习过程。

  • ：
    • 转化思想：将复杂问题、陌生问题通过某种方式，变成简单问题、熟悉问题来解决。
    • 应用场景：计算不规则图形的面积、计算分数加减法（通分）、推导公式等。
  • 学习重点与难点：
    • 重点：体会“转化”策略的价值。
    • 难点：在具体问题中主动运用“转化”策略。
  • 学习建议：
    • 学习时，多思考“这个问题可以变成我们学过的什么问题？”
    • 总结哪些地方用到了转化思想,形成自己的知识网络。

第七单元：圆和扇形的认识（部分版本）

  • ：
    1. 扇形的认识：由圆心角和半径所围成的图形。
    2. 圆心角：顶点在圆心的角。
    3. 扇形的特征：它是圆的一部分。
  • 学习重点与难点：
    • 重点：认识扇形,知道圆心角决定扇形的大小。
    • 难点：理解扇形与圆的关系。

第八单元：总复习

对全册知识进行系统梳理、巩固和提升。

学习建议

  1. 课前预习：粗读课本，了解将要学习什么，找出自己不理解的地方,带着问题听课。
  2. 认真听讲：紧跟老师的思路，特别是概念、公式和例题的讲解过程。
  3. 勤于思考：多问“为什么”，理解知识的来龙去脉,而不是死记硬背。
  4. 规范作业：书写工整，步骤清晰,养成良好的学习习惯。
  5. 及时复习：每天课后花少量时间回顾当天所学内容,每周进行一次小结。
  6. 善用错题本：记录错题，分析错误原因，定期回顾,避免再犯。

希望这份详细的总结能对您和孩子有所帮助！祝学习顺利！

小学五年级下册数学书苏教版
（图片来源网络，侵删）