人教版六年级上册数学该怎么学？-小学教育-育材教育咨询

整体概述

六年级上册是人教版小学数学的最后一个学期,是整个小学阶段数学知识的深化和提升，本册教材不仅包含新的核心知识，更重要的是为即将升入初中的学生打下坚实的基础，培养他们的数学思维能力和解决复杂问题的能力。

（图片来源网络，侵删）

本册教材的主要内容可以分为四大板块：

分数乘法：作为六年级的起点，是分数运算的基础。
位置与方向：在五年级的基础上，用更精确的坐标表示位置。
分数除法：分数运算的另一大核心，与乘法互为逆运算。
比：引入一种新的关系表达方式，与分数、除法密切相关。
圆：学习曲线图形的第一个内容，涉及周长和面积的计算。
百分数：在分数基础上，学习应用更广泛的表示“率”的数。
统计：认识扇形统计图，学习从数据中获取信息。
数学广角——鸡兔同笼：经典的逻辑问题，培养学生的假设推理能力。

各单元核心知识点详解

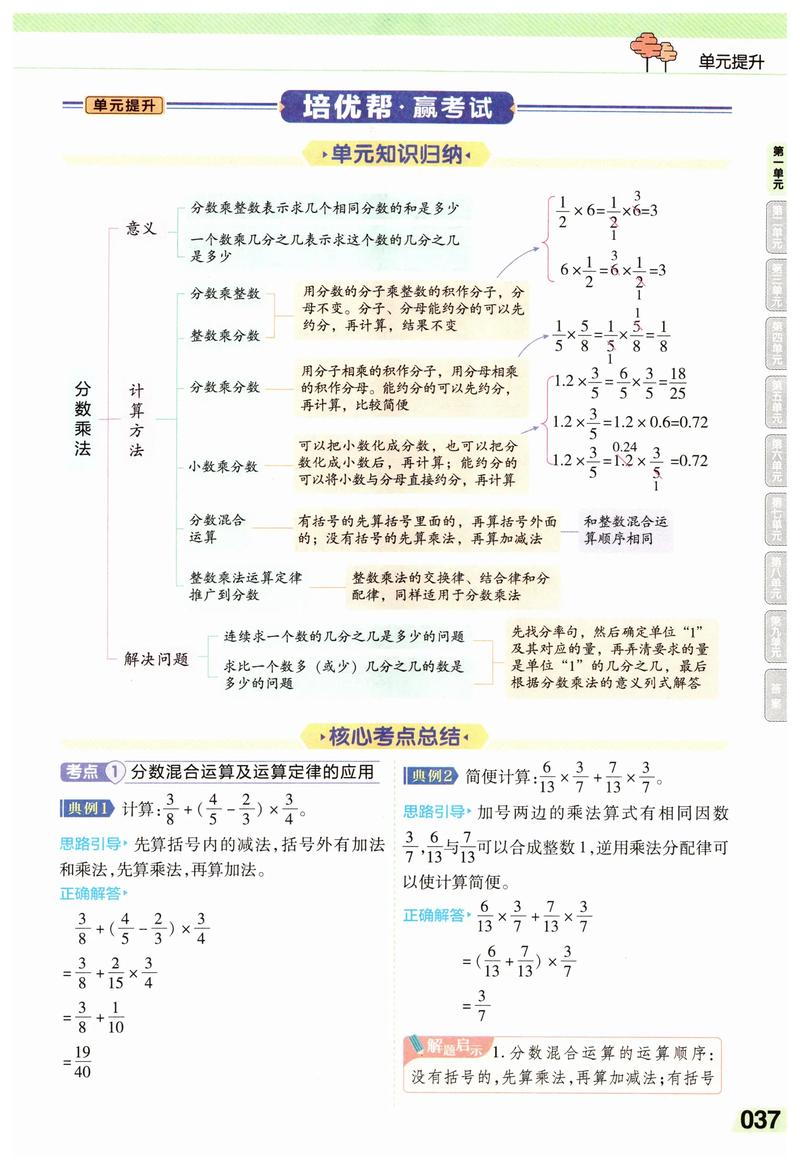
第一单元：分数乘法

：
1. 分数乘整数：计算法则（分子与整数相乘，分母不变），意义（求几个相同分数的和的简便运算）。
2. 分数乘分数：计算法则（分子相乘作分子，分母相乘作分母），意义（求一个数的几分之几是多少）。
3. “求一个数的几分之几是多少”的应用题：这是本单元的重点和难点，是分数乘法最重要的应用，解题关键：找准单位“1”的量，用单位“1”的量 × 所求量占单位“1”的几分之几。
4. 倒数的认识：乘积是1的两个数互为倒数，1的倒数是1，0没有倒数。
5. 混合运算：整数乘法运算定律（交换律、结合律、分配律）同样适用于分数乘法。
学习重点：
- 理解并掌握分数乘法的计算法则。
- 能熟练解决“求一个数的几分之几是多少”的应用题。
学习难点：
（图片来源网络，侵删）
- 理解分数乘法的意义,特别是分数乘分数的意义。
- 在复杂的应用题中准确判断单位“1”。
- 灵活运用乘法运算定律进行简便计算。

第二单元：位置与方向

：
- 用数对表示物体的位置，格式：（列数, 行数）。
- 根据方向和距离确定物体的位置,需要先确定观测点（中心点），再描述方向（如：北偏东30°），最后说明距离。
学习重点：
- 掌握用数对确定位置的方法。
- 能根据方向和距离描述路线图或物体位置。
学习难点：
- 理解“北偏东”、“南偏西”等方向的描述方法。
- 在动态的路线描述中,准确区分观测点和目标点。

第三单元：分数除法

：
（图片来源网络，侵删）
1. 分数除法：计算法则（除以一个不为0的数，等于乘这个数的倒数）。
2. “已知一个数的几分之几是多少，求这个数”的应用题：这是本单元的重点，也是分数除法的核心应用，解题关键：设单位“1”的量为未知数x，根据等量关系列方程求解，或者用除法（已知量 ÷ 对应分率）。
3. 比的意义：两个数相叉又比，表示两个数相除的关系。
4. 比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变。
5. 化简比和求比值：化简比是根据基本性质，将比化成最简单的整数比；求比值是前项除以后项，得到一个数（分数、小数或整数）。
6. 按比例分配：把一个量按照一定的比进行分配。
学习重点：
- 掌握分数除法的计算方法。
- 解决“已知一个数的几分之几是多少，求这个数”的应用题。
学习难点：
- 理解分数除法的算理,特别是为什么“除以一个数等于乘它的倒数”。
- 区分分数乘法和除法应用题,找准单位“1”和等量关系。
- 理解比与分数、除法的关系（a:b = a÷b = a/b）。

第四单元：比

：
- （此单元内容已在第三单元“分数除法”中详细阐述，是分数除法的延伸和应用）
- 比的意义、基本性质、化简比、求比值、按比例分配。
学习重点：
- 理解比的意义,掌握比的基本性质。
- 能解决按比例分配的实际问题。
学习难点：
- 将生活中的“份数”关系转化为“比”的关系。
- 解决复杂的按比例分配问题。

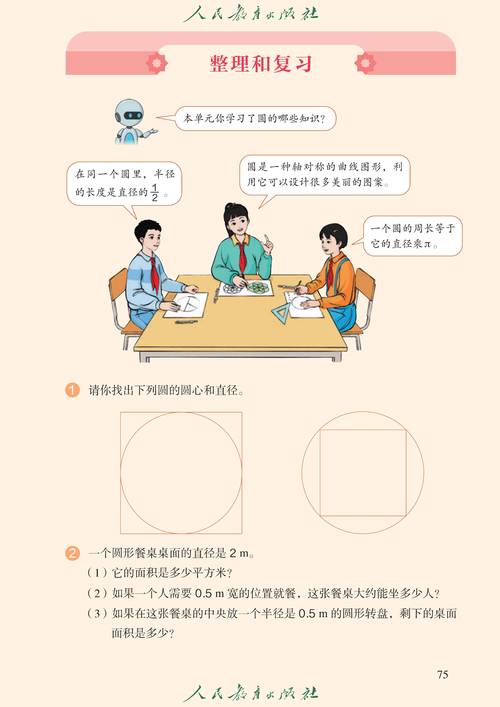
第五单元：圆

：
1. 圆的认识：圆心（决定圆的位置）、半径（决定圆的大小）、直径（d=2r）、半径和直径的关系。
2. 圆的周长：围成圆的曲线的长度，公式：C = πd 或 C = 2πr。π (圆周率) 是一个无限不循环小数，约等于3.14。
3. 圆的面积：圆所占平面的大小，公式：S = πr²，推导过程：通过“化曲为直”、“化圆为方”的思想，将圆切割拼成一个近似的长方形。
4. 半圆的周长与面积：半圆的周长 = πr + 2r；半圆的面积 = πr² / 2。
5. 圆环的面积：S = π(R² - r²)。
学习重点：
- 掌握圆的周长和面积的计算公式。
- 能运用公式解决与圆相关的实际问题。
学习难点：
- 理解圆周率π的意义。
- 理解圆面积公式的推导过程。
- 解决组合图形（如正方形内最大的圆、圆内最大的正方形）的周长和面积问题。

第六单元：百分数

：
1. 百分数的意义：表示一个数是另一个数的百分之几，它只表示两个数的倍比关系，不带单位。
2. 百分数与小数、分数的互化：
  - 小数化百分数：小数点向右移动两位，添上%。
  - 百分数化小数：小数点向左移动两位，去掉%。
  - 分数化百分数：通常先化成小数，再化成百分数。
  - 百分数化分数：先写成分母是100的分数，再化简。
3. 百分率（求一个数是另一个数的百分之几）：如：出勤率、成活率、合格率等，公式：(部分量 ÷ 总量) × 100%。
4. 百分数应用题：
  - 求一个数的百分之几是多少（单位“1”的量已知）：用乘法。
  - 已知一个数的百分之几是多少，求这个数（单位“1”的量未知）：用方程或除法。
  - 求一个数比另一个数多（或少）百分之几：用相差的量 ÷ 单位“1”的量。
学习重点：
- 理解百分数的意义。
- 熟练进行百分数、小数、分数的互化。
- 解决各类百分数应用题。
学习难点：
- 区分“增加了百分之几”和“增加到百分之几”。
- 在折扣、成数、税率、利率等实际问题中，准确找到单位“1”和等量关系。

第七单元：统计

：
- 扇形统计图：用整个圆表示总数，用圆内各个扇形的大小表示各部分数量占总数的百分比。
- 特点：能很清楚地表示出各部分数量同总数之间的关系。
学习重点：
- 能看懂扇形统计图,从中获取信息。
- 根据数据制作简单的扇形统计图。
学习难点：

理解扇形统计图中“百分比”与“具体数量”的转换。

第八单元：数学广角——鸡兔同笼

：
- 经典问题：笼子里有若干只鸡和兔，从上面数，有35个头；从下面数，有94只脚，求鸡和兔各有多少只？
- 解决方法：
  1. 列表法：逐一尝试，适合数据较小的情况。
  2. 假设法：假设全是鸡或全是兔，然后根据脚的数量差进行调整，这是核心方法。
  3. 方程法：设未知数x，根据“鸡的脚数 + 兔的脚数 = 总脚数”列方程求解。
学习重点：

掌握用“假设法”解决“鸡兔同笼”问题。
学习难点：

理解假设法的算理,即为什么可以通过调整假设来解决问题。

学习建议

夯实基础，狠抓计算：分数乘除法是本册的核心，计算必须准确、迅速，每天进行几道口算和笔算练习，形成肌肉记忆。
理解概念，抓住关键：对于“单位‘1’”、“比的意义”、“百分数的意义”等核心概念，一定要深刻理解，而不仅仅是死记硬背，可以多举生活中的例子来帮助理解。
画图辅助，化繁为简：遇到复杂的应用题，不要急于列式，先画出线段图，把抽象的数量关系变得直观，这是解决分数、百分数应用题的“万能钥匙”。
归纳总结，形成体系：将分数、除法、比、百分数之间的联系和区别进行归纳整理。a : b = a ÷ b = a/b (b≠0)，这能帮助你将零散的知识串联成网。
联系生活，学以致用：数学来源于生活，多观察生活中的数学问题，如购物折扣、储蓄利息、家庭支出等，尝试用学到的数学知识去解决它们，增加学习的趣味性和成就感。
勤于思考，多问为什么：对于公式、法则，不仅要记住“怎么算”，更要思考“为什么这么算”，思考圆面积公式的推导过程，能让你对知识的理解更上一层楼。

六年级上册的内容是小学阶段的“压轴”戏，难度和深度都有所增加，只要同学们紧跟老师的步伐，勤加练习，善于思考，一定能顺利掌握，为初中数学的学习打下坚实的基础。