小学六年级上册数学核心知识点总结
六年级上册的数学是整个小学阶段的重点和难点,内容多,综合性强,为初中数学学习打下坚实的基础,主要可以分为以下几个大模块:

(图片来源网络,侵删)
第一单元:分数乘法
这是本册的开篇,也是后续学习的基础。
分数乘整数
- 意义:求几个相同加数的和的简便运算。
3/4 + 3/4 + 3/4就是求3个3/4的和,可以列式为3/4 × 3。 - 计算方法:用分子乘整数的积作分子,分母不变,计算结果要化成最简分数。
- 举例:
3/4 × 3 = (3×3)/4 = 9/4
- 举例:
- 应用:求一个数的几倍是多少。
分数乘分数
- 意义:求一个数的几分之几是多少,这是分数乘法的核心意义。
- 举例:
1/2 × 1/4表示求1/2的1/4是多少。
- 举例:
- 计算方法:用分子相乘的积作分子,分母相乘的积作分母,计算结果要化成最简分数。
- 举例:
2/3 × 3/4 = (2×3)/(3×4) = 6/12 = 1/2
- 举例:
- 技巧:可以先约分,再计算,使数据变小,计算更简便。
- 举例:
2/3 × 3/4可以先约分,2/3和3/4中的3约掉,变成2/1 × 1/4 = 2/4 = 1/2。
- 举例:
“求一个数的几分之几是多少”的应用题

(图片来源网络,侵删)
- 核心关系:单位“1” × 分率 = 对应量。
- 解题关键:找准单位“1”(即“占”、“是”、“比”等词后面的量),然后用乘法计算。
- 举例:一根绳子长
10米,用去了3/5,用去了多少米?- 分析:单位“1”是绳子的总长
10米,求用去的长度,就是求10米的3/5是多少。 - 列式:
10 × 3/5 = 6(米)。
- 分析:单位“1”是绳子的总长
- 举例:一根绳子长
倒数的认识
- 定义:如果两个数的乘积是
1,那么这两个数互为倒数。- 举例:
2和1/2互为倒数,3/4和4/3互为倒数。
- 举例:
- 求倒数的方法:
- 真分数的倒数是假分数(如
2/3的倒数是3/2)。 - 假分数的倒数是真分数或整数(如
5/2的倒数是2/5,4/1的倒数是1/4)。 - 整数的倒数是
1除以这个数(如5的倒数是1/5)。 1的倒数是1,0没有倒数。
- 真分数的倒数是假分数(如
第二单元:位置与方向
在六年级上册主要以“用数对确定位置”为主。
用数对确定位置
- 方法:用
(列数, 行数)的形式表示。- 举例:教室里,小明的位置在第
3列第4行,可以表示为(3, 4)。
- 举例:教室里,小明的位置在第
- 特点:
- 列数从左往右数,行数从前往后数。
- 数对
(x, y)中的x表示列,y表示行。 - 两个数对,如果数对中的第一个数相同,表示它们在同一列;如果第二个数相同,表示它们在同一行。
第三单元:分数除法
本单元是分数运算的另一个重点,与分数乘法紧密相关。
(图片来源网络,侵删)
分数除法的意义
- 意义:分数除法是分数乘法的逆运算,已知两个数的积和其中一个因数,求另一个因数。
- 举例:
3/4 ÷ 2表示已知两个因数的积是3/4,其中一个因数是2,求另一个因数是多少。
- 举例:
分数除以整数
- 计算方法:除以一个不为
0的整数,等于乘这个整数的倒数。- 举例:
3/4 ÷ 2 = 3/4 × 1/2 = 3/8
- 举例:
一个数除以分数
- 计算方法:一个数除以分数,等于乘这个分数的倒数。
- 举例:
2 ÷ 2/3 = 2 × 3/2 = 3 - 分数除法的统一法则是“除以一个数(不为0),等于乘这个数的倒数”。
- 举例:
“已知一个数的几分之几是多少,求这个数”的应用题
- 核心关系:对应量 ÷ 分率 = 单位“1”。
- 解题关键:找准单位“1”,用除法计算,这是与分数乘法应用题最显著的区别。
- 举例:一堆煤,用去了
3/5,还剩下12吨,这堆煤原来有多少吨?- 分析:单位“1”是这堆煤的总量,未知,用去的分率是
3/5,剩下的分率是1 - 3/5 = 2/5。12吨对应的分率是2/5。 - 列式:
12 ÷ (1 - 3/5) = 12 ÷ 2/5 = 12 × 5/2 = 30(吨)。
- 分析:单位“1”是这堆煤的总量,未知,用去的分率是
- 举例:一堆煤,用去了
比和按比例分配
- 比的意义:两个数相叉又比,表示两个数相除的关系。
3:4读作3比4,表示3除以4。 - 比的基本性质:比的前项和后项同时乘或除以一个相同的数(不为0),比值不变。
- 化简比:利用比的基本性质,把比化成最简单的整数比。
- 举例:
12:18 = (12÷6):(18÷6) = 2:3
- 举例:
- 求比值:比的前项除以后项。
- 举例:
12:18 = 12 ÷ 18 = 2/3
- 举例:
- 按比例分配:把一个总量按照一定的比来进行分配。
- 解题步骤:
- 求总份数(比的前、后项之和)。
- 求每份的量(总量 ÷ 总份数)。
- 求各部分的量(每份的量 × 各部分所占的份数)。
- 举例:将
60本图书按3:2的比例分给甲、乙两个班,各分得多少本?- 总份数:
3 + 2 = 5 - 每份的量:
60 ÷ 5 = 12(本) - 甲班:
12 × 3 = 36(本),乙班:12 × 2 = 24(本)
- 总份数:
- 解题步骤:
第四单元:圆
本单元是几何图形的重点,需要熟练掌握公式。
圆的认识
- 圆心 (O):决定圆的位置。
- 半径:连接圆心和圆上任意一点的线段,决定圆的大小,在同一个圆里,半径有无数条,且长度都相等。
- 直径:通过圆心并且两端都在圆上的线段,在同一个圆里,直径有无数条,且长度都相等,直径是半径的
2倍,d = 2r或r = d/2。 - 圆的周长:围成圆的曲线的长度。
- 圆周率 (π):任意一个圆的周长与它的直径的比值,是一个固定的无限不循环小数,约等于
1415926...,小学阶段通常取14。 - 圆的周长公式:
C = πd或C = 2πr- 举例:一个圆的半径是
5厘米,它的周长是多少?C = 2 × 3.14 × 5 = 31.4(厘米)
- 举例:一个圆的半径是
- 圆的面积:圆所占平面的大小。
- 圆的面积公式:
S = πr²(r 是半径)- 推导:通过“化曲为直”、“化圆为方”的思想,将圆等分成若干份,拼成一个近似的长方形,长方形的长是圆周长的一半
(πr),宽是圆的半径。 - 举例:一个圆的直径是
10分米,它的面积是多少?- 半径
r = 10 ÷ 2 = 5(分米) S = 3.14 × 5² = 3.14 × 25 = 78.5(平方分米)
- 半径
- 推导:通过“化曲为直”、“化圆为方”的思想,将圆等分成若干份,拼成一个近似的长方形,长方形的长是圆周长的一半
圆环的面积
- 定义:两个半径不相等的同心圆之间的部分。
- 面积公式:
S_环 = S_大 - S_小 = π(R² - r²)(R 是大圆半径,r 是小圆半径)
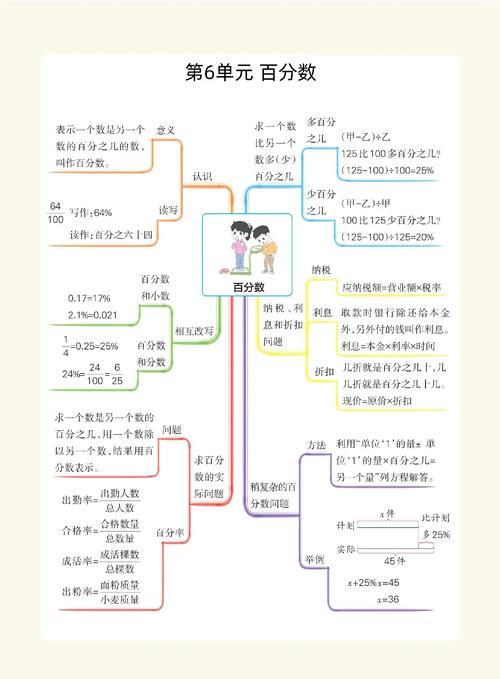
第五单元:百分数
百分数是分数的一种特殊形式,应用非常广泛。
百分数的意义和读写
- 意义:表示一个数是另一个数的百分之几,它只表示两个数的倍比关系,后面不带单位。
- 读写:百分号“%”。
- 举例:
50%读作“百分之五十”。
- 举例:
百分数与小数、分数的互化
- 小数化百分数:小数点向右移动两位,加上 。
- 举例:
25 = 25%
- 举例:
- 百分数化小数:去掉 ,小数点向左移动两位。
- 举例:
120% = 1.2
- 举例:
- 分数化百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再化成百分数。
- 举例:
3/4 = 0.75 = 75%
- 举例:
- 百分数化分数:先把百分数改写成分母是
100的分数,再化简。- 举例:
60% = 60/100 = 3/5
- 举例:
百分数的应用题
- 基本类型:
- 求一个数是另一个数的百分之几(求分率)。
- 公式:
部分量 ÷ 单位“1” = 百分率 - 举例:全班
50人,有10人是三好学生,三好学生占全班的百分之几?10 ÷ 50 = 0.2 = 20%
- 公式:
- 求一个数的百分之几是多少(求部分量)。
- 公式:单位“1” × 百分率 = 部分量
- 举例:一根绳子长
20米,用去了40%,用去了多少米?20 × 40% = 20 × 0.4 = 8(米)
- 已知一个数的百分之几是多少,求这个数(求单位“1”)。
- 公式:部分量 ÷ 百分率 = 单位“1”
- 举例:一条裤子打
8折后是160元,原价是多少元?160 ÷ 80% = 160 ÷ 0.8 = 200(元)
- 求一个数是另一个数的百分之几(求分率)。
- 其他常见问题:合格率、出勤率、成活率等,计算方法都是
(合格数 ÷ 总数) × 100%,折扣、纳税、利息等实际问题也属于百分数应用。
第六单元:统计
本单元主要学习扇形统计图。
扇形统计图的特点
- 特点:用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分比。
- 优点:可以很清楚地表示出各部分数量同总数之间的关系。
扇形统计图的绘制与解读
- 绘制:先计算各部分占总数的百分比,再计算每个扇形对应的圆心角(
360° × 百分比),然后用量角器画出各个扇形。 - 解读:能从图中直接读出各部分所占的百分比,并进行比较和分析。
第七单元:数学广角——鸡兔同笼
主要是培养孩子的逻辑思维和解决问题的策略思想。
问题模型
- 经典问题:笼子里有若干只鸡和兔,从上面数,有
35个头;从下面数,有94只脚,问鸡和兔各有多少只?
解题方法
- 假设法(核心方法):
- 假设全是鸡:
- 脚的总数:
35 × 2 = 70(只) - 比实际少的脚数:
94 - 70 = 24(只) - 每只兔比鸡多
4 - 2 = 2(只)脚 - 兔的只数:
24 ÷ 2 = 12(只) - 鸡的只数:
35 - 12 = 23(只)
- 脚的总数:
- 假设全是兔:
- 脚的总数:
35 × 4 = 140(只) - 比实际多的脚数:
140 - 94 = 46(只) - 每只鸡比兔少
4 - 2 = 2(只)脚 - 鸡的只数:
46 ÷ 2 = 23(只) - 兔的只数:
35 - 23 = 12(只)
- 脚的总数:
- 假设全是鸡:
- 方程法:
- 设鸡有
x只,兔有(35 - x)只。 - 列方程:
2x + 4(35 - x) = 94 - 解方程:
2x + 140 - 4x = 94,-2x = -46,x = 23。 - 所以鸡有
23只,兔有12只。
- 设鸡有
学习建议
- 夯实基础:分数的乘除运算是所有后续知识的基础,必须做到熟练、准确。
- 理解概念:不要死记硬背公式,要理解每个公式背后的意义(如圆面积公式的推导)。
- 多做练习:特别是应用题,要通过不同题型的练习,学会分析数量关系,找准单位“1”。
- 归纳总结:将易错点、典型题、解题技巧整理成笔记,定期回顾。
- 联系生活:百分数、圆等知识在生活中应用广泛,多观察生活中的例子,可以帮助更好地理解。
希望这份总结能帮助您的孩子系统地复习六年级上册的数学知识!


